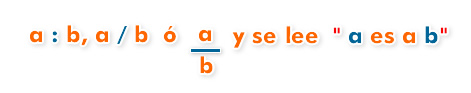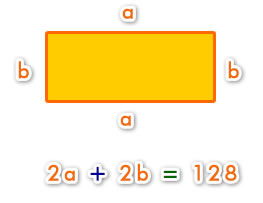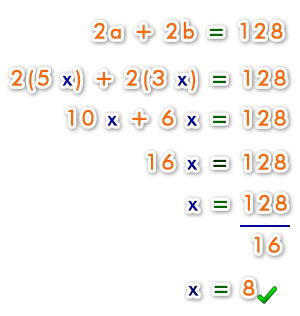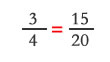1- Razón

Una razón es una comparación entre dos o más cantidades. Puede expresarse mediante una fracción. Si las cantidades a comparar son  a y b, la razón entre ellas se escribe como:

 

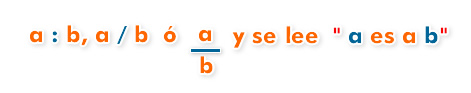
Ejemplo:

En una sala de clases hay 10 mujeres y 18 hombres. ¿Qué relación numérica existe entre el número de mujeres y el número de hombres?

La relación entre el número de mujeres y el número de hombres es de  "10 es a 18" , otra forma de leerlo es "10 de 18 "

 

El término a es el antecedente de la razón y el b, el consecuente.

 

 

El resultado de la división o cociente entre el antecedente y el consecuente se denomina valor de la razón

  

Dos o más razones son equivalentes cuando tienen igual valor.

 

1.1- Resolución de problemas:

Veamos cómo resolver problemas de razones:

Ejemplo 1:

La edad de 2 personas están en la relación de 5 a 9 y la suma de ellas es 84. Hallar las edades.

Solución:

Si las edades son a y b

Cuando nos hablan de relación o razón entre dos cantidades sabemos que nos están hablando de una comparación entre dos cantidades. Por lo tanto expresamos los datos como una razón:

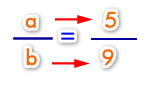
Ahora volvemos a los datos del problema:

Nos indican que la suma de los 2 números nos tiene que dar 84. Esto se expresa así:

 

Ahora lo que debemos hacer es trabajar con una constante, que en este caso será " X" . Por lo tanto :

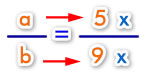
Reemplazando los datos en la ecuación tenemos:

 

Ahora que tenemos el valor de x podemos reemplazar para obtener los valores de a y b :

 

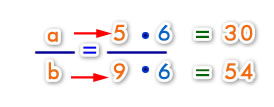
Respuesta: Por lo tanto podemos decir que las edades son 30 y 54.

 

Ejemplo 2:

El perímetro de un rectángulo mide 128 cm, y la razón entre las medidas de sus lados es 5: 3. Calcula el área del rectángulo.

Solución:

Siguiendo el procedimiento del problema anterior planteamos el problema en una ecuación. Sabemos que el perímetro de un rectángulo es igual a la suma de todos sus lados:

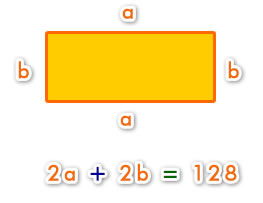
Si expresamos las variables dadas en el problema:

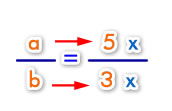
Ahora reemplazamos y resolvemos:

 

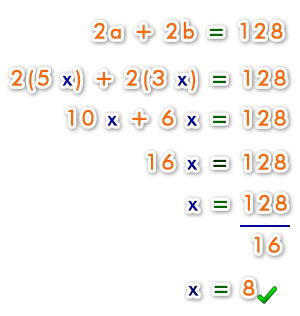
Con este resultado reemplazamos :

 

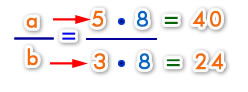
Ahora no nos debemos olvidar que nos están pidiendo el área del rectángulo. Sabemos que el área del rectángulos se calcula :

A = a • b

Por lo tanto la respuesta sería :

A = 40 • 24  = 960

Respuesta: El área del rectángulo es 960 cm²

 

Otra forma de resolver razones es siguiendo los siguientes pasos:

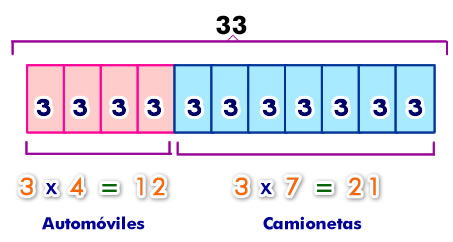
Respuesta: Hay 12 automóviles

 

Ahora resuelve los siguientes problemas, siguiendo los pasos anteriores: (haz clic tres veces para comprobar tu respuesta)

 

2- Proporciones

Una proporción es la igualdad de dos razones.

 

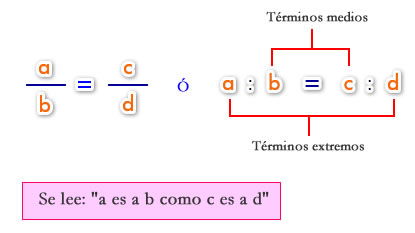
2.1- Propiedad fundamental 

En toda proporción, el producto de los términos medios es igual al producto de los términos extremos (Teorema fundamental de las proporciones). Es decir:

 

3- Regla de tres

La regla de tres es un procedimiento que consiste en encontrar el cuarto término de una proporción, a la que solo se le conocen tres términos. 

 

Ejemplo: Encuentra el valor de X, para que las razones formen una proporción:

Puede ser simple cuando solamente intervienen en ella dos variables o compuesta cuando intervienen tres o más variables.

Toda regla de tres presenta una incógnita y una hipótesis. La hipótesis está constituida por los datos del problema que se conocen y la incógnita por el dato que se busca.

Veamos el siguiente ejemplo:

Las edades de un hijo y su madre están en la razón 2 : 5. Si la edad de la madre es 45 años, ¿cuál es la edad del hijo?

Se puede plantear una proporción y al aplicar la regla de 3 se determina la edad del hijo.

$\frac{x}{45}=\frac{2}{5}$
 

$$\begin{gathered} x · 5 = 45 · 2 \\ 5x = 90 \\ x = \frac{90}{5} \\ x = 18 \end{gathered}$$

Entonces, la edad del hijo es 18 años.

 

De acuerdo a la relación con la incógnita, puede ser directa cuando los aumentos en una variable provocan aumento en la otra variable o inversa cuando los aumentos en una variable provocan disminución en la otra variable.