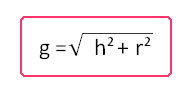1- ¿Qué son los cuerpos geométricos?
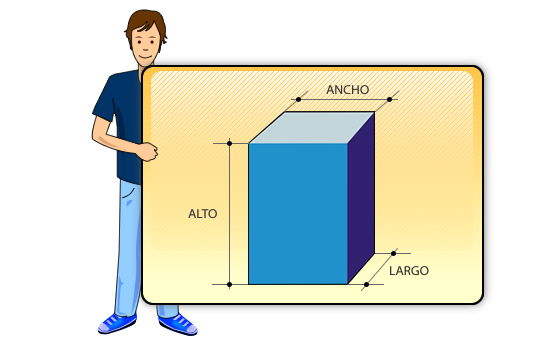
Un sólido o cuerpo geométrico es una figura geométrica de tres dimensiones (largo, ancho y alto), que ocupa un lugar en el espacio y en consecuencia tiene un volumen.
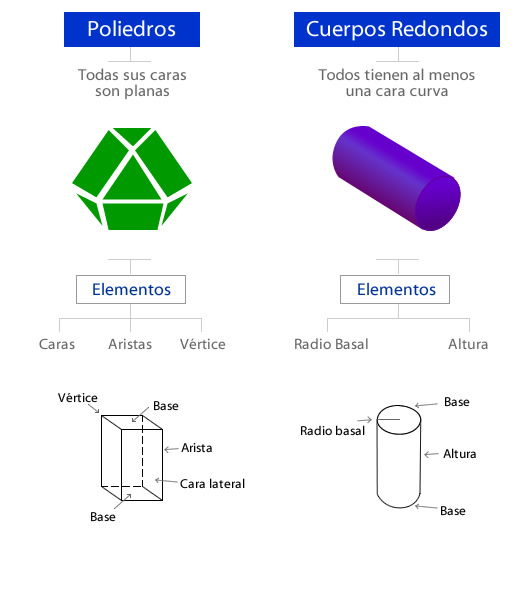
Los cuerpos geométricos pueden ser: Poliedros y Cuerpos Redondos.
2- Poliedros
La palabra poliedro proviene del griego y significa muchas caras. Los poliedros son cuerpos geométricos cuyas caras son todas polígonos (figuras geométricas planas). Por lo tanto tienen todas sus caras planas. Los elementos de un poliedro son caras, aristas y vértices.
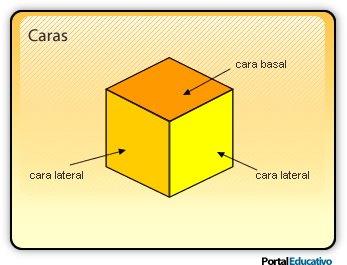
2.1- Caras
Son las superficies planas que forman el poliedro, las cuales se interceptan entre sí.
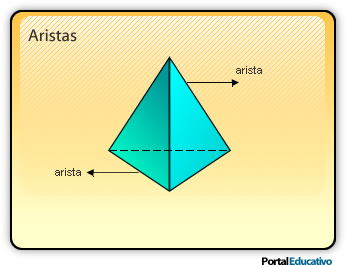
2.2- Aristas
La línea que une dos caras se denomina arista. Por ejemplo en un cubo hay 12 aristas.
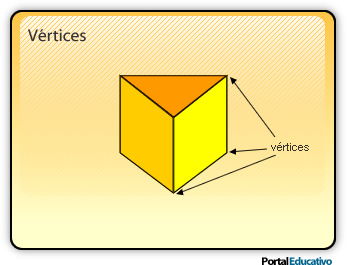
2.3- Vértices
Son los puntos donde se interceptan 3 o más aristas.
3- Clases de poliedros
Se distinguen dos clases de poliedros:
- Los poliedros regulares: son aquellos cuyas caras son todas polígonos regulares iguales y coincide el mismo número de ellas en cada vértice.
- Los poliedros irregulares: Los poliedros son irregulares cuando los polígonos (figuras geométricas planas) que lo forman, no son todos iguales (por ejemplo, una piedra preciosa tallada, o los caireles de una lámpara).
La representación gráfica de los cuerpos geométricos en general, presenta la dificultad de que, teniendo tres dimensiones, solamente pueden representarse en el plano dos dimensiones; por lo cual se recurre a una técnica de dibujo, la perspectiva, que permite dar la sensación tridimensional.
3.1- Los poliedros regulares
Existen solo cinco poliedros regulares: Tetraedro, Cubo, Octaedro, Dodecaedro e Icosaedro.
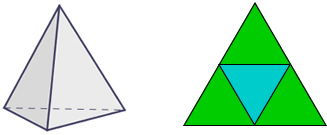
A- El tetraedro
Compuesto por cuatro caras con forma de triángulos equiláteros. Tiene cuatro vértices y seis aristas.
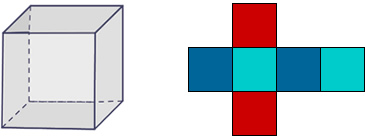
B- El cubo
Está compuesto por seis caras cuadradas; motivo por el cual se le conoce también con el nombre de hexaedro regular, (hexaedro = cuerpo con 6 caras). Tiene 8 vértices y 12 aristas.
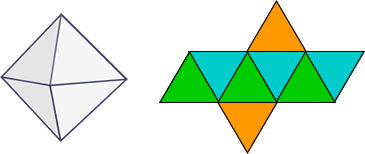
C- El octaedro
Compuesto por ocho caras con forma de triángulos equiláteros, en forma de dos pirámides unidas por sus base. Tiene 6 vértices y 12 aristas.
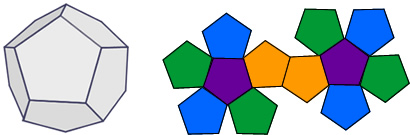
D- El dodecaedro
Compuesto por doce caras con forma de pentágono. Tiene 20 vértices y 30 aristas.
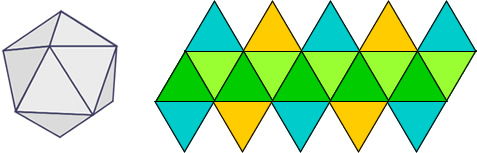
E- El icosaedro
Compuesto por veinte caras con forma de triángulos equiláteros, que tiene un eje plano hexagonal.
Tiene 12 vértices y 30 aristas.
3.2- Clasificación de poliedros irregulares:
Los poliedros irregulares se clasifican básicamente en:
- Prisma
- Pirámide
Los prismas y pirámides son cuerpos geométricos cuyas caras son todas polígonos.
Los prismas tienen dos caras paralelas e iguales, llamadas bases, el resto de sus caras son paralelogramos. Las pirámides tienen una base y el resto de las caras son triángulos.
A- El prisma
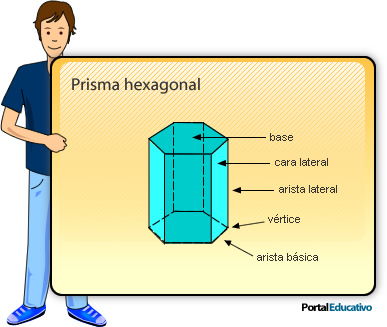
Está constituido por dos bases poligonales e iguales y sus caras laterales son paralelogramos. Según el número de lados de la base se le da el nombre al prisma.
Por ejemplo: Prismas triangular (sus bases son un triángulo), Prismas cuadrangulares (sus bases son cuadrados), Prisma pentagonal (sus bases son pentágonos), Prisma hexagonal (sus bases son hexágonos), etc.
La altura de un prisma es la distancia entre las bases.
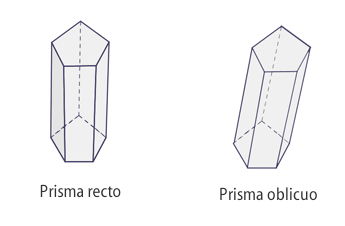
El prisma es recto cuando su eje es perpendicular a las bases y oblicuo cuando el ángulo entre el eje y la base es diferente a base 90°. Si el prisma es cortado de tal manera que la sección producida no sea paralela a una de sus bases, recibe el nombre de prisma truncado.
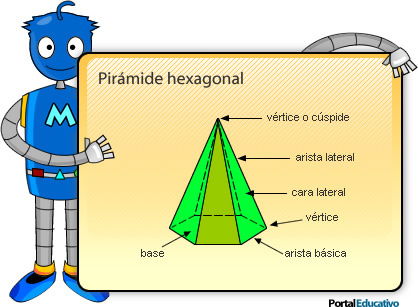
B- La pirámide
Es una figura tridimensional constituida por una base poligonal y por caras laterales cuyas aristas concurren a un punto del espacio llamado cúspide o vértice común, por lo tanto las caras laterales siempre serán triangulares. El eje o altura de la pirámide es la línea que va del vértice al centro de la base.
La apotema lateral de una pirámide regular es la altura de cualquiera de sus caras laterales.
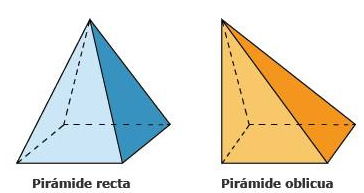
La pirámide se llama rectangular cuando el eje es perpendicular al centro de la base, en un caso diferente se llama oblicua. La porción de pirámide comprendida entre la base y la sección producida por un plano que corta sus caras laterales se llama tronco de la pirámide o pirámide truncada.
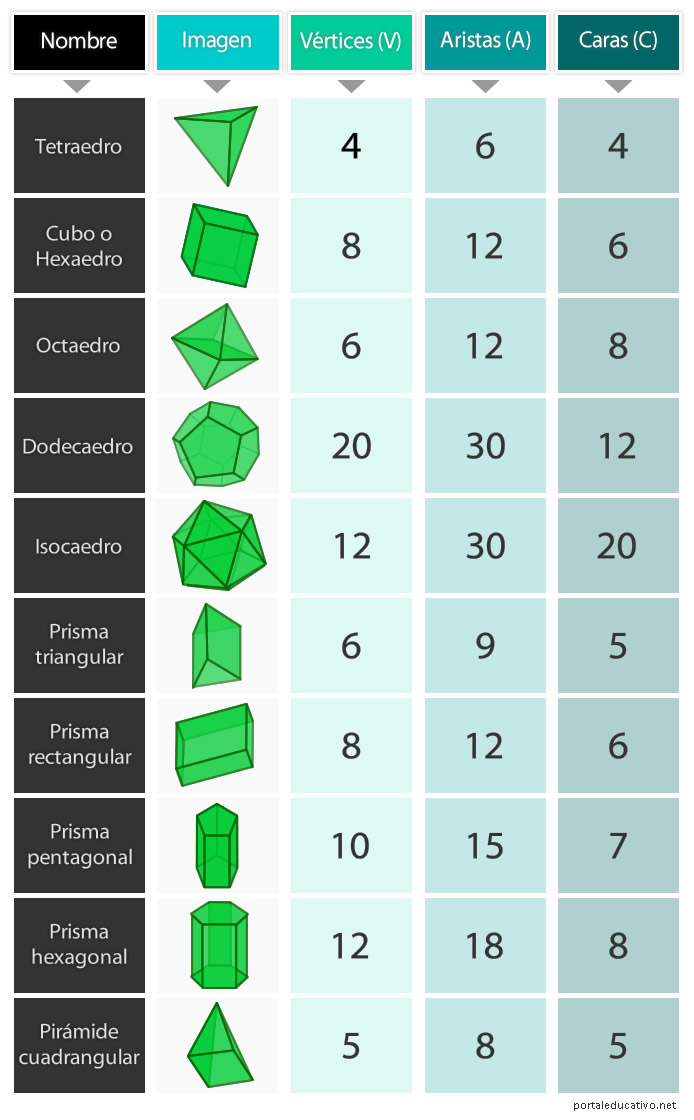
4- Cuadro comparativo: Caras, aristas y vértices de los poliedros
En el siguiente cuadro podrás ver una comparación de los elementos de cada poliedro:
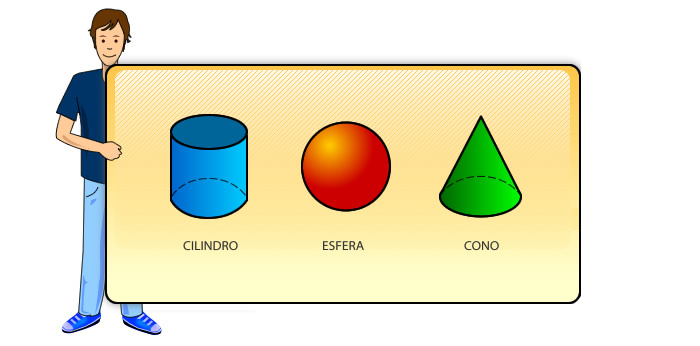
5- Cuerpos redondos
Son cuerpos geométricos compuestos total o parcialmente por figuras geométricas curvas; como por ejemplo el cilindro, la esfera o el cono.
El cilindro, el cono y la esfera son cuerpos redondos .
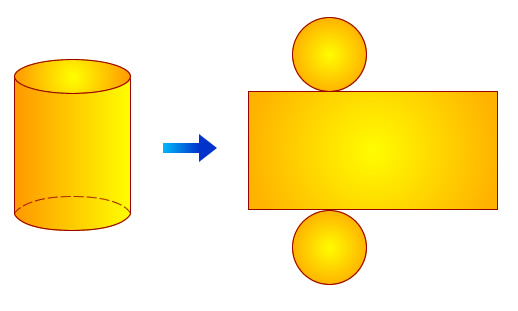
5.1- El cilindro
Un cilindro es una superficie cilíndrica que se forma cuando una recta , denominada generatriz, gira alrededor de otra recta paralela, denominada eje.
También lo podemos definir como el cuerpo que se genera cuando un rectángulo gira alrededor de un de sus lados. El cilindro tiene dos bases circulares y una superficie curva.
5.1.1- Elementos del cilindro
Por medio del dibujo de arriba, es posible determinar los elementos de un cilindro, que son: eje, bases, altura y generatriz.
- Eje: lado AD, alrededor del cual gira el rectángulo.
- Bases: son los círculos paralelos y congruentes que se generan al girar los lados AB y CD del rectángulo. Cada uno de estos lados es el radio de sucírculo y también, el radio del cilindro.
- Altura: corresponde al mismo eje AD; es perpendicular a las bases y llega al centro de ellas. Esta es la razón por la que el cilindro es recto.
- Generatriz: es el lado BC, congruente con el lado AD, y que al girar forma la cara lateral o manto del cilindro.
- Radio: el radio de los círculos que forman las bases también es el radio del cilindro.
- Centro: es el centro de cada una de las bases circulares.
El cilindro tiene 2 caras basales planas, paralelas y congruentes. 1 cara lateral que es curva y 2 aristas basales. Puedes observar que en el desarrollo en el plano se forma un rectángulo para la cara lateral, cuyos lados son el perímetro de la circunferencia que forma las bases y la altura o generatriz.
5.2- El cono
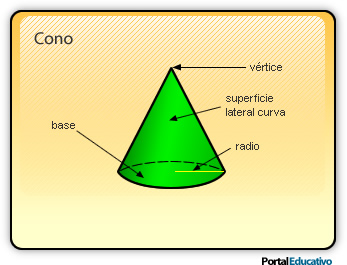
El cono es un cuerpo geométrico generado por un triángulo rectángulo al girar en torno a uno de sus catetos. El cono tiene una base circular y una superficie curva.
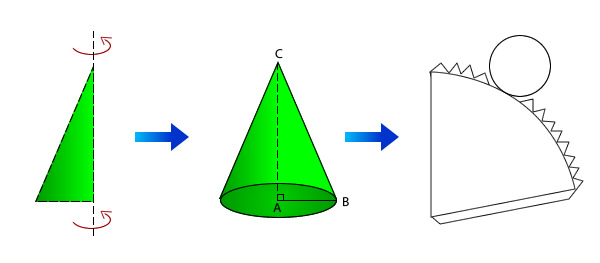
5.2.1- Elementos del cono
En el dibujo de arriba podemos distinguir los elementos de un cono recto:
- Eje: es el cateto AC. Alrededor de él gira el triángulo rectángulo.
- Base: es el círculo que genera la rotación del otro cateto, AB. Por lo tanto AB es el radio del cono. La base se simboliza: O (A, AB).
- Generatriz: es la hipotenusa del triángulo rectángulo, BC, que genera la región lateral conocida como manto del cono.
- Altura: corresponde al eje del cono, porque une el centro del círculo con la cúspide siendo perpendicular a la base.
- Centro: Es el centro de la base.
El cono tiene una cara basal plana y una cara lateral curva. Posee una arista basal y un vértice llamado cúspide.
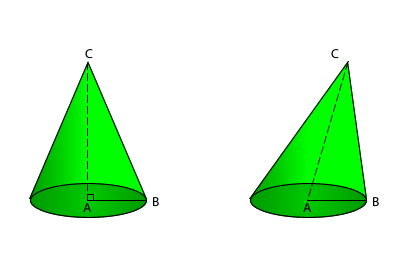
5.2.2- Tipos
Si la altura coincide con su eje, el cono es recto. Si el eje y la altura no coinciden, el cono es oblicuo.
5.3- Esfera
La esfera es el sólido generado al girar una semicircunferencia alrededor de su diámetro.
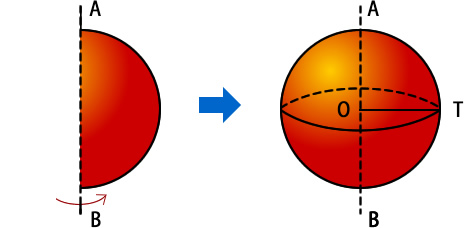
5.3.1- Elementos de la esfera
Al girar el semicírculo alrededor del diámetro AB, se genera una superficie esférica donde se determinan los siguientes elementos:
- Generatriz: es la semicircunferencia que genera la superficie esférica.
- Centro de la esfera: es el centro de la semicircunferencia y corresponde al punto O.
- Radio de la esfera: es el radio de la semicircunferencia: OA.
- Diámetro de la esfera: es el segmento que une 2 puntos opuestos de la superficie esférica, pasando por el centro: AB.
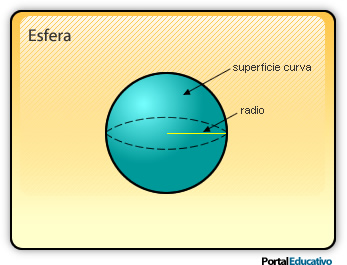
La esfera tiene una sola cara curva. Todos los puntos que forman la superficie esférica equidistan de uno fijo llamado centro, y que corresponde al centro de la semicircunferencia que gira.
5.3.2- Cortes
Una esfera puede ser cortada por un plano que pasa por su centro. De esta forma se obtienen 2 semiesferas y el plano deja como borde un círculo máximo.
Veamos la ilustración:
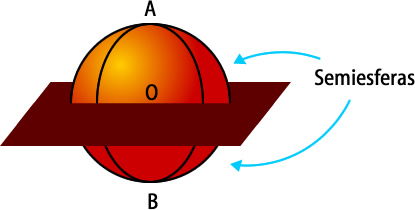
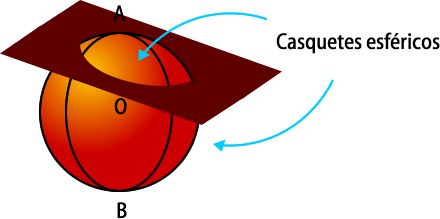
Si el plano corta a la esfera sin pasar por su centro se obtienen 2 casquetes esféricos.
Veamos un ejemplo:
6- Formulario área y volumen cuerpos geométricos
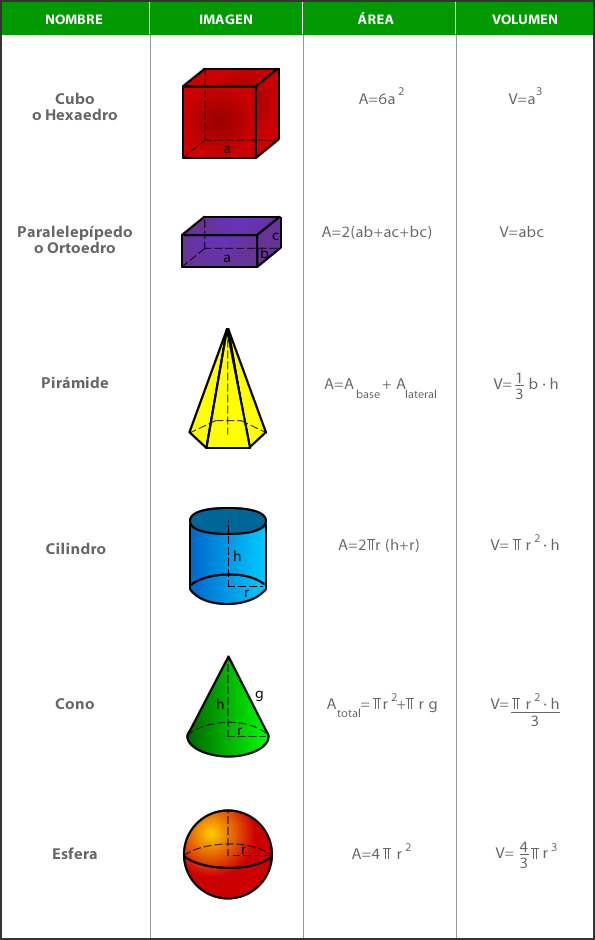
En la siguiente ilustración podrás ver las distintas fórmulas para obtener el área y volumen de los cuerpos geométricos.
7- Definición de volumen y capacidad
- Volumen: es la medida del espacio que ocupa un cuerpo
- Capacidad: es la medida del volumen que puede contener un cuerpo.
Como en general estas medidas son iguales, se suele calcular la capacidad mediante la fórmula del volumen. La medida universal del volumen es el metro cúbico (m3), existiendo los múltiplos y submúltiplos de esta medida.
8- Generatriz
Debes saber que:
8.1- Generatriz del cilindro
El cilindro es un cuerpo de revolución engendrado por un rectángulo al girar en torno a uno de sus lados, que será la altura del cilindro y el lado opuesto será la generatriz.
Por tanto la altura del cilindro será igual a la generatriz.
h = g
Donde:
h= altura
g= generatriz
8.2- Generatriz del cono
El cono es un cuerpo de revolución generado por un triángulo rectángulo al girar en torno a uno de sus catetos, que será la altura del cono y la hipotenusa será la generatriz.
Por el teorema de Pitágoras la generatriz del cono será igual a:
g2 = h2 + r2
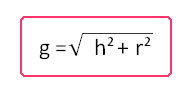
donde:
g = generatriz
h = altura
r = radio