1- Números primos
Un número a es primo si solo tiene como divisores el 1 y él mismo. Para saber si un número es primo hallamos sus divisores y si únicamente tiene dos divisores, el 1 y él mismo, entonces dicho número es primo.
Los primeros números primos son: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89 y 97.
Ejemplo: Si calculamos los divisores de 19.
Div. (19) = { 1 , 19 } → 19 sólo tiene dos divisores, así pues es un número primo.
2- Números compuestos
Un número es compuesto cuando no es primo, es decir, cuando tiene más de dos divisores.
Ejemplo: Div. (33) = { 1 , 3 , 11 , 33 } → 33 tiene más de dos divisores, por lo tanto es un número compuesto.
- El número 1 no se considera ni primo ni compuesto. Cualquier otro número natural o bien es primo o bien es compuesto.
- El 2 es el único número primo y par a la vez.
3- Cómo averiguar si un número es primo
Para averiguar si un número es primo o compuesto, se divide por la serie de números primos 2, 3, 5, 7, 11, ... hasta llegar a una división cuyo cociente sea igual o menor que el divisor. Si todas las divisiones tienen el resto distinto de cero, el número propuesto es un número primo.
Ejemplo: Vamos a ver si el número 101 es un número primo.
• 101 no es divisible por 2.
• 101 no es divisible por 3.
• 101 no es divisible por 5.
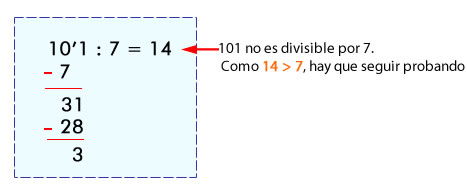
- Si dividimos el número 101 por 7:
- Si dividimos 101 por 11:
→ Entonces:
Basta con dividir el número por los números primos menores que él hasta llegar a un cociente menor que el divisor.
Si ninguna de estas divisiones es exacta, el número es primo.
Si alguna de las divisiones es exacta el número es compuesto y podemos interrumpir el proceso.
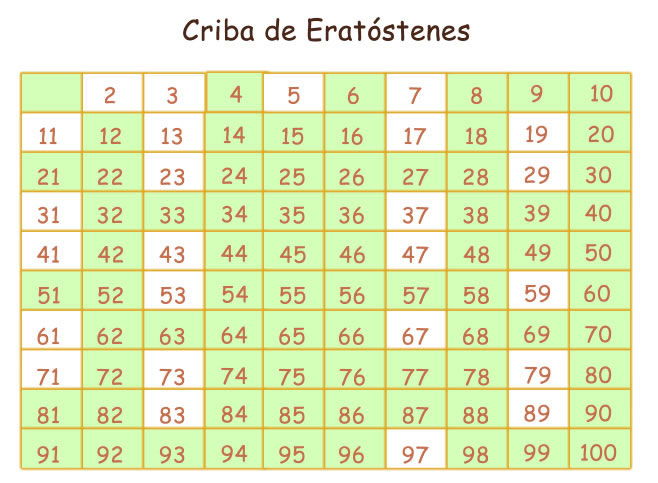
4- Criba de Eratóstenes
La criba de Eratóstenes es un algoritmo que permite hallar todos los números primos menores que un número natural dado n. Se forma una tabla con todos los números naturales comprendidos entre 2 y n, y se van tachando los números que no son primos de la siguiente manera: Comenzando por el 2, se tachan todos sus múltiplos; comenzando de nuevo, cuando se encuentra un número entero que no ha sido tachado, ese número es declarado primo, y se procede a tachar todos sus múltiplos, así sucesivamente. El proceso termina cuando el cuadrado del mayor número confirmado como primo es mayor que n.
- Números primos y compuestos
Contacto comercial
Envíanos un mensaje
Llámanos al +56233247872
Escríbenos por Facebook
