1- Dinámica del movimiento circular 

Se dice que un objeto que se mueve en una trayectoria circular con rapidez constante $\overrightarrow{v}$? experimenta un movimiento circular uniforme. En este caso, la magnitud de la velocidad permanece constante; pero la dirección de la velocidad cambia continuamente conforme el objeto se mueve alrededor del círculo.

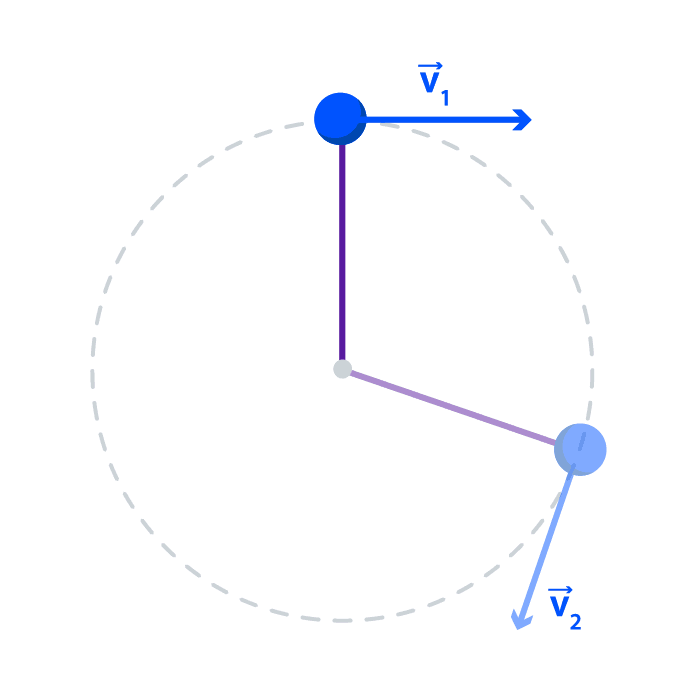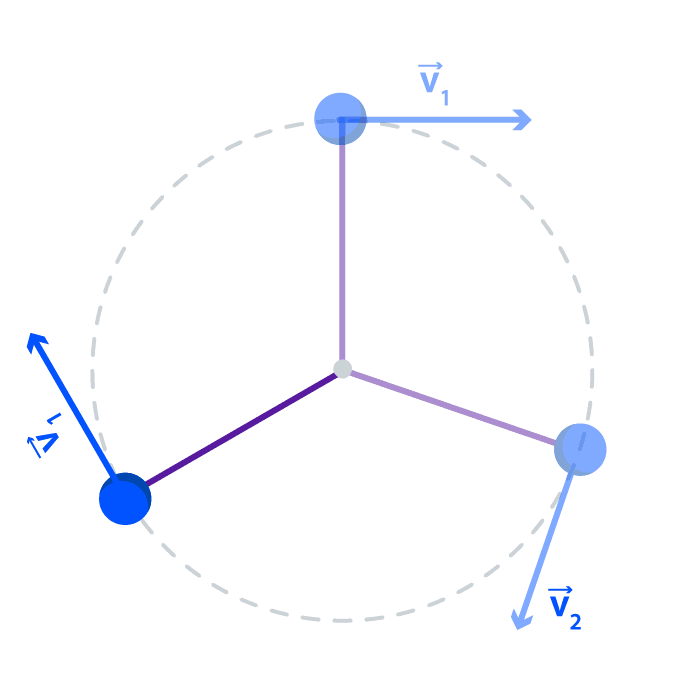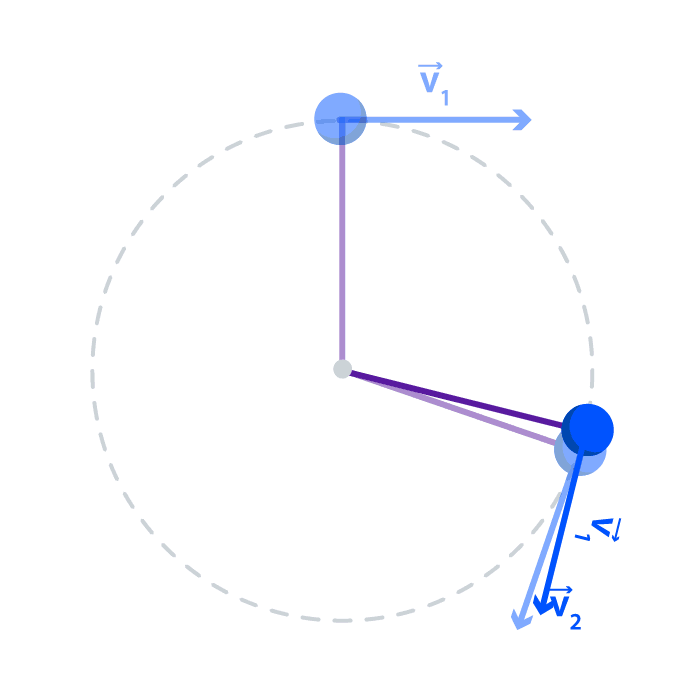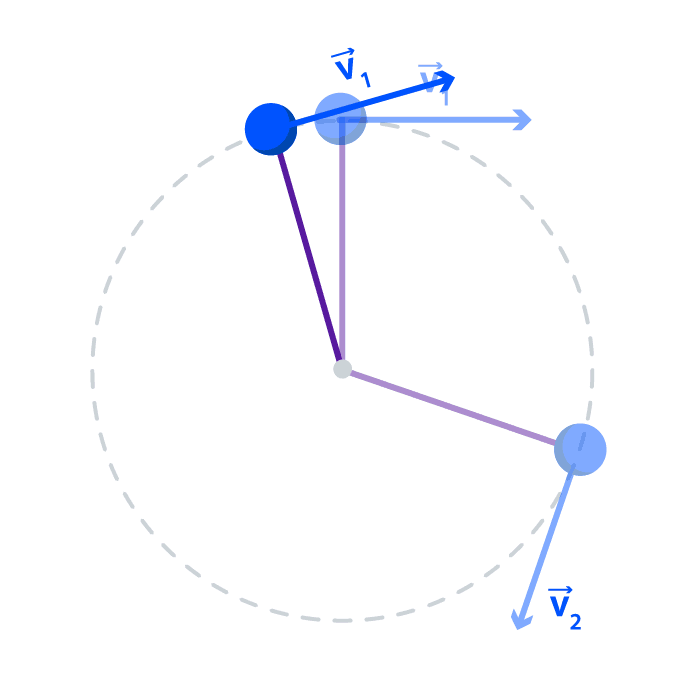
Si trasladamos este mismo ejemplo al Carrusel de Fantasilandia observándolo desde arriba, podemos notar como el vector velocidad va cambiando su dirección constantemente apuntando siempre hacia donde está mirando el caballo. Sin embargo el módulo de la velocidad no cambia, permanece constante.

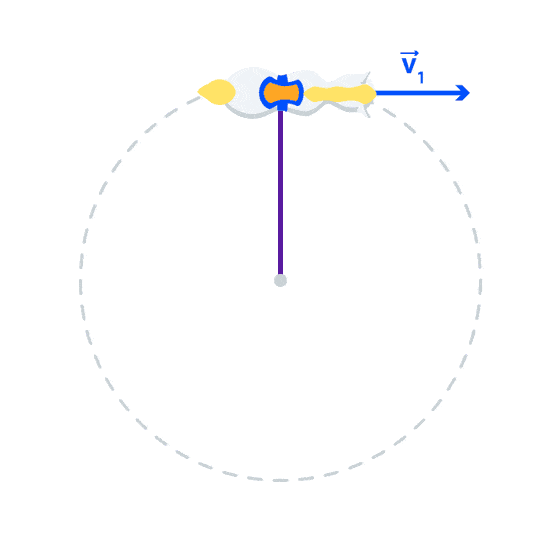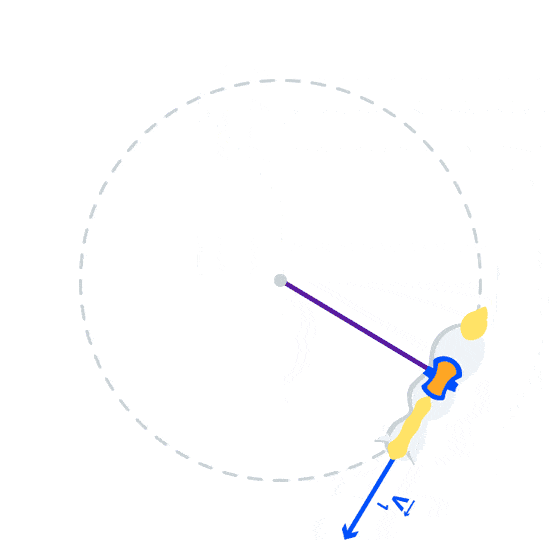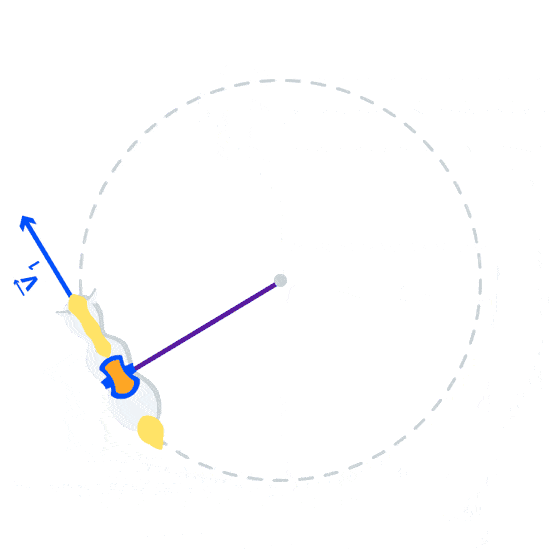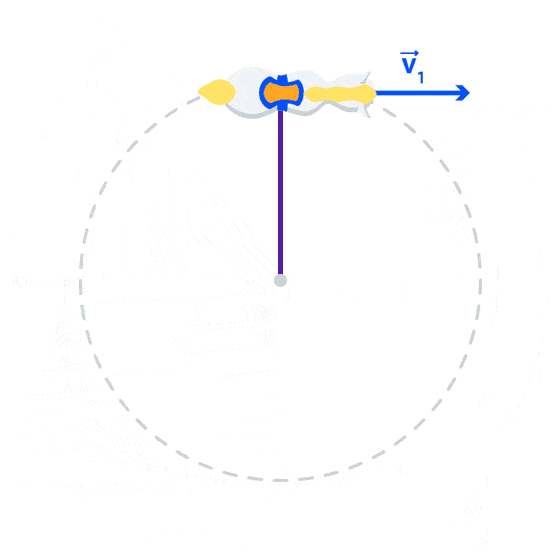
Dado que la aceleración se define como la tasa del cambio de la velocidad, un cambio en la dirección de esta última implica una aceleración, así como un cambio en la magnitud de la velocidad también implica una aceleración. Así, un objeto que describe una trayectoria circular está acelerando constantemente, aun cuando la rapidez permanece constante ($\stackrel{\rightharpoonup }{v_1}=\stackrel{\rightharpoonup }{v_2}=\stackrel{\rightharpoonup }{v}$).

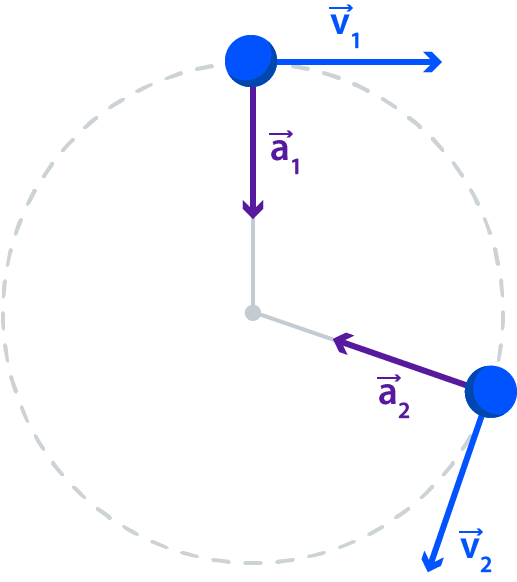
En el estudio del movimiento circular uniforme MCU, hemos visto que la velocidad del móvil no cambia de módulo pero cambia constantemente de dirección. 

El móvil tiene una aceleración que está dirigida hacia el centro de la trayectoria, denominada aceleración normal y cuyo módulo es:

Esto es un objeto que se mueve en un círculo de radio r con rapidez constante v tiene una aceleración que está dirigida hacia el centro del círculo y cuya magnitud está dada por la expresión anterior. 

No debe sorprender que esta aceleración dependa de v y de r. Cuanto mayor sea la rapidez v, más rápido cambiará de dirección la velocidad; y cuanto mayor sea el radio, más lento cambiará de dirección la velocidad.

El vector aceleración apunta hacia el centro del círculo; sin embargo, el vector velocidad siempre apuntará en la dirección de movimiento, que es tangencial al círculo.

Así, los vectores de velocidad y de aceleración son perpendiculares entre sí, en cada punto de la trayectoria para el movimiento circular uniforme. 
 

A menudo al movimiento circular se le describe en términos de la frecuencia f, es decir, el número de revoluciones por segundo. El periodo T de un objeto que se mueve en una trayectoria circular es el tiempo requerido para completar una revolución. El periodo y la frecuencia están relacionados por

Por ejemplo, si un caballito en el Carrusel gira con una frecuencia de 3$\left[\frac{rev}{s}\right]$, entonces cada revolución tarda $\frac{1}{3}$ segundos. Para un objeto que da vueltas en un círculo (de circunferencia $2\mathrm{\pi r}$) con rapidez constante v, podemos escribir:

Puesto que en una revolución el objeto recorre una circunferencia.

De acuerdo al segundo principio de Newton, si un objeto está acelerado debe haber una fuerza neta no nula actuando sobre él. Un objeto que se mueve en un círculo, como una pelota atada al extremo de una cuerda, debe tener una fuerza aplicada sobre el objeto para seguir moviéndose en ese círculo. Es decir, es necesaria una fuerza neta para darle una aceleración centrípeta. La magnitud de la fuerza neta requerida puede calcularse usando el segundo principio Newton para la componente radial,

donde ${\alpha }_{radial}$ es la aceleración centrípeta y $\sum _{}^{}{F}_{radial}$ es la fuerza total (o fuerza neta) en la dirección radial.

Para el movimiento circular uniforme (v= constante), la aceleración es ${\alpha }_{radial}$, que apunta hacia el centro del círculo en cualquier momento. Así, la fuerza neta también debe estar dirigida hacia el centro del círculo. 

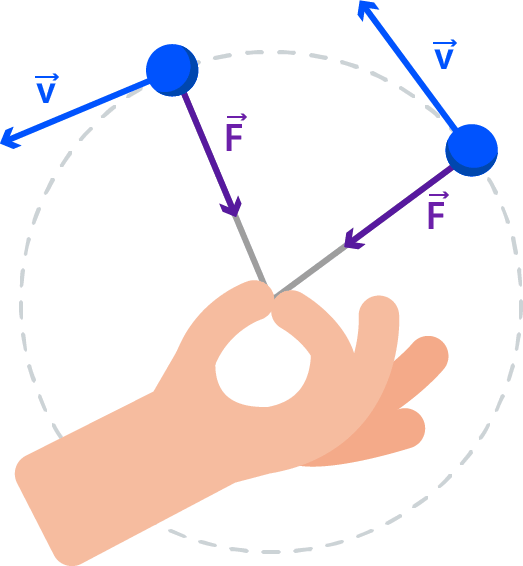
Es necesaria una fuerza neta porque, si no hubiera una fuerza neta ejercida sobre el objeto, este no se movería en un círculo sino en una línea recta, como nos lo indica el primer principio de Newton. La dirección de la fuerza cambia continuamente, de manera que siempre está dirigida hacia el centro del círculo. Esta fuerza se llama a veces fuerza centrípeta (“que apunta hacia el centro”). Pero esté consciente de que “fuerza centrípeta” no significa algún nuevo tipo de fuerza. El término únicamente describe la dirección de la fuerza neta necesaria para producir una trayectoria circular: la fuerza neta está dirigida hacia el centro del círculo. La fuerza debe ser aplicada por otros objetos. Por ejemplo, para hacer girar una pelota atada al extremo de una cuerda, usted jala la cuerda y esta ejerce una fuerza sobre la pelota.

Ejemplo:

¿A qué rapidez mínima debe viajar el carro del juego mecánico Boomerang cuando esté de cabeza en la parte superior de un círculo, de manera que no caigan los pasajeros? Considere un radio con curvatura de 7,6 [m].
 

Respuesta: 

Si hiciéramos un diagrama de cuerpo libre con los jóvenes en la parte superior de círculo tendríamos la imagen siguiente.
 

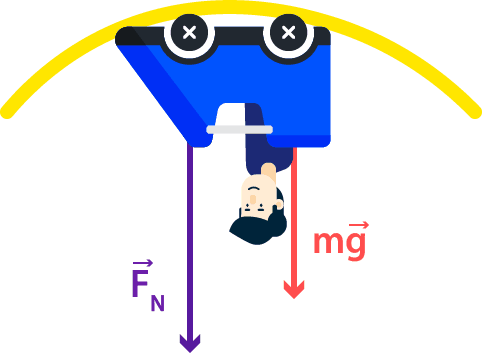
La fuerza normal entre el carro y la superficie empuja hacia abajo a los pasajeros, tal como se muestra en el diagrama. Suponemos que no hay dispositivos de seguridad accionados. Se elige la dirección positiva hacia abajo y escribimos el segundo principio de Newton para los pasajeros. 

$$\begin{gathered} \sum _{}^{}F=F_N+mg=m\alpha \\ {F}_N+mg=m·\frac{v^2}{R} \\ {F}_N=m·\frac{v^2}{R}-mg \\ {F}_N=m·\left(\frac{v^2}{R}-g\right) \end{gathered}$$

De esta expresión podemos ver que para una velocidad alta, la fuerza normal será positiva lo que significa que los pasajeros están en contacto con el móvil. 

Pero a medida que disminuye la velocidad, la fuerza normal también disminuye. Si la fuerza normal se convierte en 0, los pasajeros ya no están en contacto con el móvil; están en caída libre.

El valor mínimo para que los pasajeros no caigan del juego se obtiene de la expresión:

$$\begin{gathered} 0=\frac{{v^2}_{min}}{R}-g \\ {v}_{min}=\sqrt{rg} \\ {v}_{min}=\sqrt{\left(9,8\left[\frac{m}{s^2}\right]\right)}(7,6[m\left]\right) \\ {v}_{min}=8,6\left[\frac{m}{s}\right] \end{gathered}$$