1- ¿Qué es el volumen?
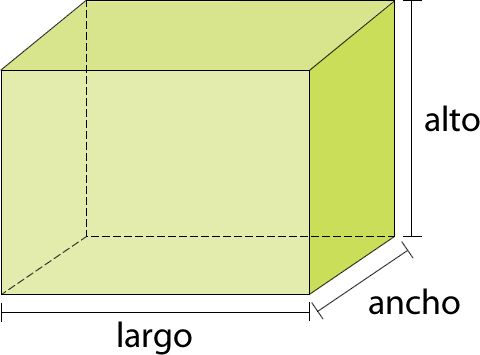
El volumen es el espacio que ocupa un cuerpo, considerando sus tres dimensiones: largo, ancho y alto.
Para medir el volumen de un cuerpo se puede utilizar una determinada unidad de medida, por ejemplo, un cubo, contando la cantidad de cubitos que forman el cuerpo.
En este caso se utiliza un cubo cuyo largo, ancho y alto miden 1 cm, por lo tanto, su volumen es 1 cm3.

El volumen del cuerpo es 24 cm3, ya que está formado por 24 cubos cuyo largo, ancho y alto miden 1 cm.
En este caso las figuras tienen diferentes medidas, pero su volumen es el mismo.

La medida universal del volumen es el metro cúbico (m3), existiendo los múltiplos (ejemplo, decámetro cúbico: dam3) y submúltiplos de esta medida (ejemplo, centímetro cúbico: cm3).
2- Volumen de un paralelepípedo
Observa la siguiente tabla con las dimensiones de 3 paralelepípedos distintos:
|
Largo
|
Ancho
|
Alto
|
Volumen
|
|
4 cm
|
2 cm
|
5 cm
|
40 cm3
|
|
5 cm
|
3 cm
|
6 cm
|
90 cm3
|
|
10 cm
|
5 cm
|
7 cm
|
350 cm3
|
¿Cuál es la relación matemática entre las medidas de cada dimensión con respecto al volumen?
Si se multiplica la medida del largo, por el ancho y por el alto se obtiene el volumen del paralelepípedo.
Analicemos el caso del paralelepípedo de 10 cm de largo, 7 cm de ancho y 5 cm de alto.
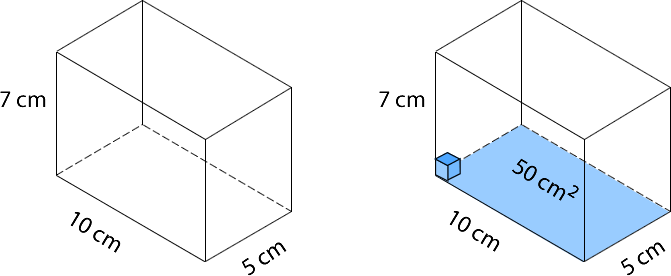
Observamos que la base es un rectángulo de 10 · 5, entonces esta se puede cubrir con 50 cubos de arista 1 cm. La cantidad de cubos de la primera capa coincide con él área de la base del paralelepípedo.
Posteriormente, observamos la medida de la altura que es equivalente a 7 cm. Entonces, hay 7 capas de 50 cubos cada una.
Por lo tanto, el volumen del paralelepípedo está dado por:
V= 10 · 5 · 7
V= 350 cm3
Como puedes ver, primero se calculó el área de la base del prisma y posteriormente su resultado se multiplicó por la medida de la altura (h). Esto se puede expresar de la siguiente manera:
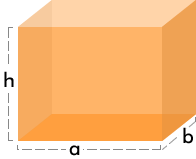
Donde:
AB = área de la base ⇒a • b
h = altura
Ejemplo 1:
Calcular el volumen (V) de un paralelepípedo de base rectangular con dimensiones de 4dm y 6 dm, respectivamente, y 15 dm de altura (h).
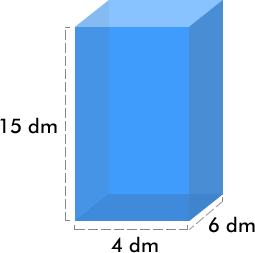
Desarrollo:
Ejemplo 2:
Calcula el volumen del siguiente paralelepípedo:

3- Volumen de un cubo
Veamos la siguiente situación:
¿Cuál es volumen del cubo considerando que cada cubo pequeño tiene un volumen de 1 cm3?
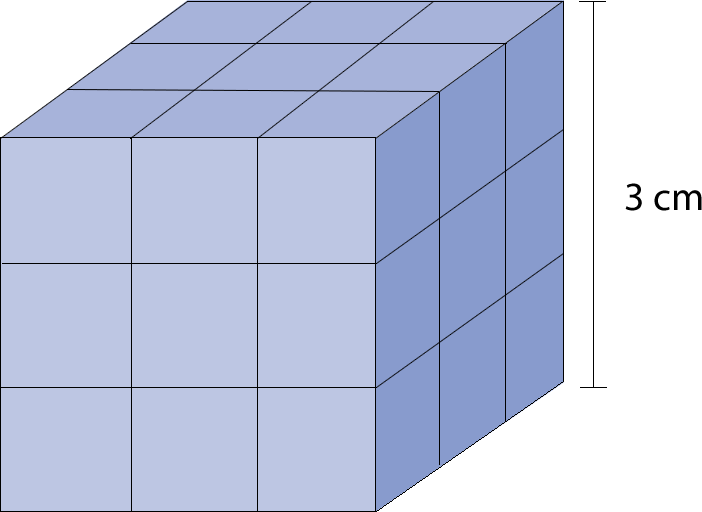
Contamos la cantidad de cubitos que forman el cuerpo y corresponde a 27 cubos, por lo tanto, su volumen es 27 cm3.
¿De qué otra forma podemos calcular el volumen del cubo?
Observa la siguiente tabla con las dimensiones de un cubo:
|
Largo
|
Ancho
|
Alto
|
Volumen
|
|
2 cm
|
2 cm
|
2 cm
|
8 cm3
|
|
3 cm
|
3 cm
|
3 cm
|
27 cm3
|
|
4 cm
|
4 cm
|
4 cm
|
64 cm3
|
¿Cuál es la relación matemática entre las medidas de cada dimensión con respecto al volumen?
Si se multiplica la medida del largo, por el ancho y por el alto del cubo se obtiene su volumen. Esto es equivalente a multiplicar 3 veces por sí misma, la medida de la arista del cubo. Por lo tanto, la expresión matemática que permite calcular el volumen de un cubo es:
Ejemplo 1: Calcula el volumen del siguiente cubo.
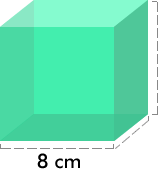
V= a · a · a
V= 8 · 8 · 8
V= 512 cm3
El volumen del cubo es de 512 cm3.
4- Resolución de problemas
4.1- ¿Cuál es el volumen de un cubo, cuya área total es 150 cm2?
Para resolver la situación se debe determinar la medida de la arista del cubo. Lo primero que se debe realizar es conocer el área de una cara del cubo, por lo que se divide el área total por 6.
150 : 6 = 25
Luego realizamos la pregunta, ¿qué número multiplicado por sí mismo da como resultado 25?
Ese número es 5, por lo tanto, la medida de la arista del cubo mide 5 cm.
Luego, aplicamos la fórmula para calcular el volumen de un cubo:
V = a · a · a
V = 5 · 5 · 5
V = 125 cm3
Respuesta: El volumen del cubo es 125 cm3.
4.2- Si el volumen de un cubo es 343 cm3, ¿cuál es la medida de sus aristas?
Para resolver este problema debemos encontrar un número que multiplicado 3 veces por sí mismo dé como resultado 343.
Buscamos el número:
4 · 4 · 4 = 64
5 · 5 · 5 = 125
6 · 6 · 6 = 216
7 · 7 · 7 = 343
Respuesta: La medida de la arista es 7 cm.
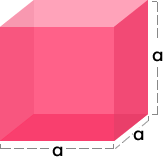
4.3- ¿Qué pasa con el volumen del siguiente cubo si la medida de su arista se duplica?
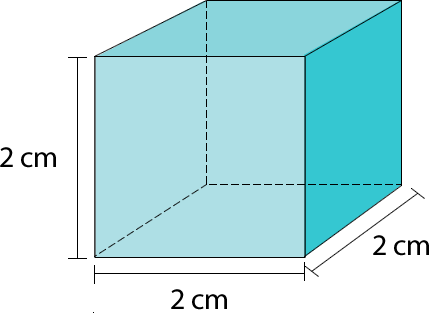
Si la arista se duplica su nuevo valor es 4 cm.
Al calcular el volumen de cada cubo, se tiene lo siguiente:
Cubo 1:
V = a · a · a
V = 2 · 2 · 2
V = 8 cm3
Cubo 2:
V = a · a · a
V = 4 · 4 · 4
V = 64 cm3
El volumen aumenta 8 veces, ya que 8 · 8 = 64.
Respuesta: Si la medida de la arista se duplica, su volumen aumenta 8 veces.
4.4- ¿Cuál es volumen de un paralelepípedo cuya altura es 9 cm y su área basal es 36 cm2?
Para calcular el volumen de un paralelepípedo se multiplica el área de la base por la altura:
V = 36 · 9
V = 324 cm3
Respuesta: El volumen del paralelepípedo es 324 cm3
4.5- El largo y el ancho de un paralelepípedo miden 6 m y 4 m respectivamente. ¿Cuál es la medida de su altura si su volumen es 192 m³?
Para conocer la altura del paralelepípedo, reemplazamos los valores conocidos en la fórmula del volumen del paralelepípedo:
V = a · b · h
192 = 6 · 4 · h
192 = 24 · h
192/24 = h
8 = h
Respuesta: La medida de la altura del paralelepípedo es 8 m.