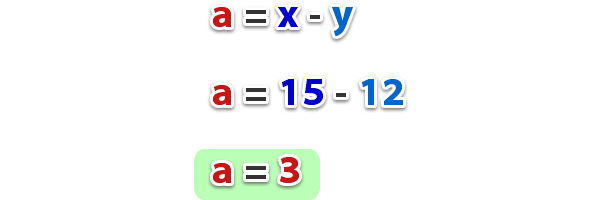1- ¿Qué es un Teorema?

Un teorema es toda proposición que partiendo de un supuesto (hipótesis), afirma una verdad (tesis) no evidente por sí misma, por lo tanto, deben ser demostradas.

El enunciado de un teorema consta de dos partes: 

- Hipótesis, que contiene los datos.

- Tesis, que es la verdad que se quiere demostrar.

El razonamiento o deducción lógica que se hace para concluir la tesis utilizando la hipótesis se llama demostración.

Existen también los lemas, que son teoremas de menor importancia, cuyo único objetivo es facilitar la demostración de otro teorema más importante.

Se llama corolario a toda consecuencia directa de un teorema que se deduce por un razonamiento simple.

Un teorema se llama recíproco de otro cuando la tesis del primero pasa a ser la hipótesis del segundo y la hipótesis del primero se convierte en la tesis del segundo.

 

2- Teoremas fundamentales sobre triángulos

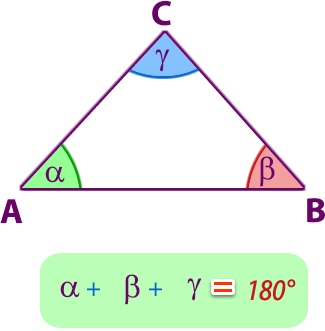
2.1- Teorema de la suma de los ángulos interiores
La suma de las medidas de los ángulos interiores de un triángulo es 180°

 

 

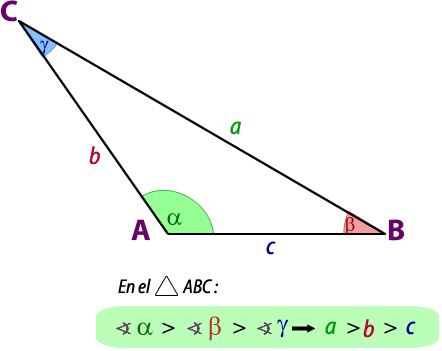
2.2- Teorema del lado mayor (propiedad de correspondencia)
En un triángulo, al lado de mayor longitud se le opone el ángulo de mayor medida y viceversa.

 

 

 

2.3- En un triángulo, a lados congruentes se oponen ángulos congruentes y a ángulos congruentes se oponen lados congruentes.

 

 

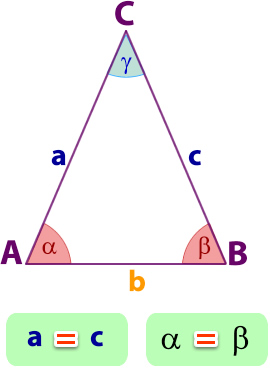
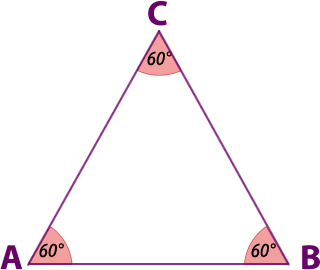
2.4- Los ángulos interiores de un triángulo equilátero miden todos 60°.

 

 

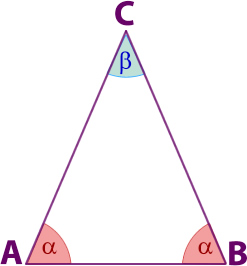
2.5- En un triángulo isósceles, los ángulos basales son congruentes.

 

 

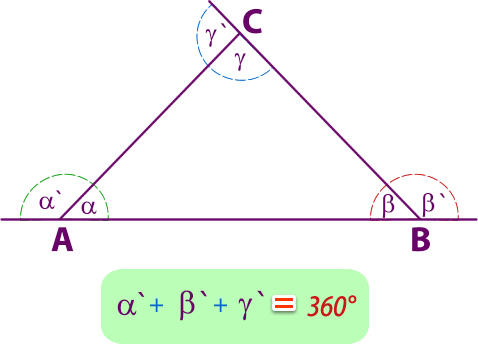
2.6- Teorema de la suma de las medidas de los ángulos exteriores
La suma de las medidas de los ángulos exteriores de un triángulo es 360°.

 

 

 

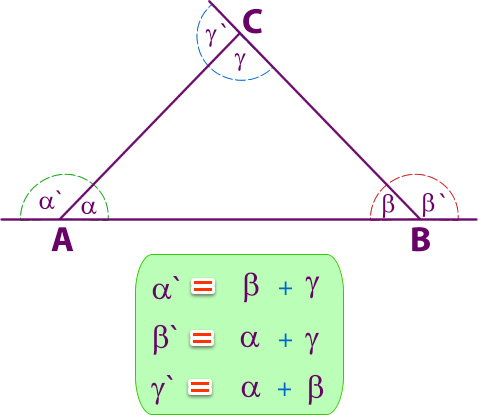
2.7- Teorema del ángulo exterior
En todo triángulo, la medida de un ángulo exterior es igual a la suma de las medidas de los ángulos interiores no adyacentes a él.

 

 

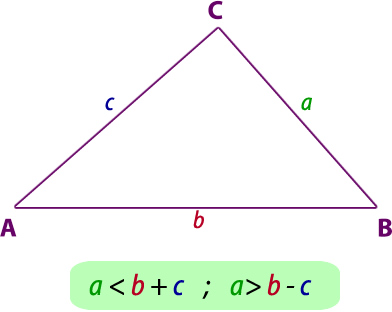
2.8- Teorema de la desigualdad triangular
Un lado de un triángulo siempre es menor que la suma de los otros dos (condición de existencia de un triángulo dados sus lados)

 

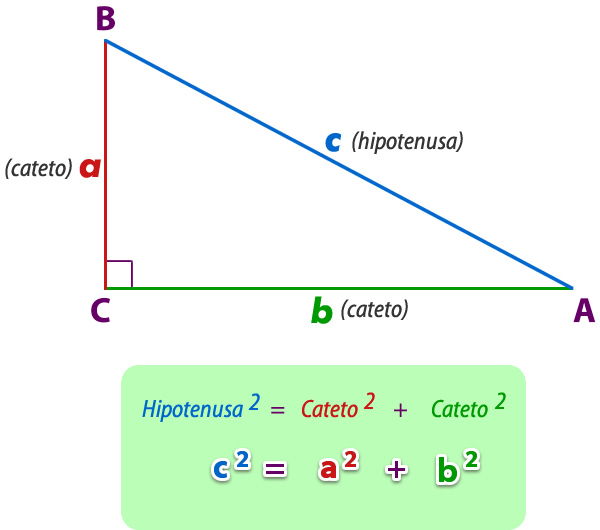
2.9- Teorema particular de Pitágoras
En todo triángulo rectángulo el cuadrado de la medida de la hipotenusa es igual a la suma de los cuadrados de las medidas de los catetos.

 

 

 

2.10- Teorema general de Pitágoras
a) En un triángulo cualquiera, el cuadrado de la medida del lado opuesto a un ángulo agudo es igual a la suma de los cuadrados de las medidas de los otros dos lados menos el doble de la medida de uno de ellos por la proyección del otro sobre él.

 

 

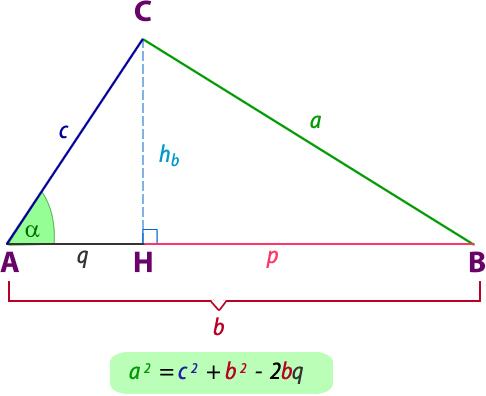
b) En un triángulo obtusángulo, el cuadrado de la medida del lado opuesto al ángulo obtuso es igual a la suma de los cuadrados de las medidas de los otros dos lados más el doble de uno de ellos por la proyección del otro sobre él.

 

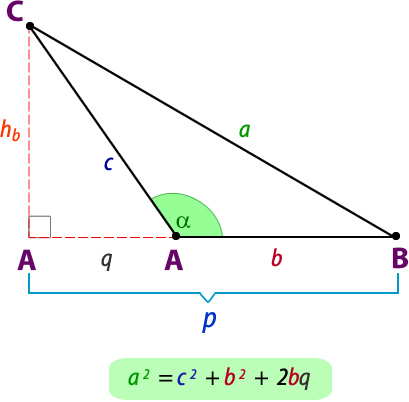
El teorema genera de Pitágoras es un criterio para determinar si un triángulo es rectángulo, acutángulo u obtusángulo cuando se conocen sus tres lados.

 

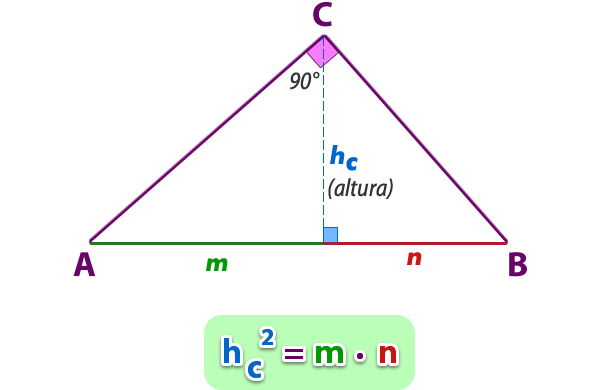
2.11- Teorema de Euclides
En todo triángulo rectángulo:

a) El cuadrado de la medida de la altura respecto de la hipotenusa es igual al producto de las proyecciones  de los catetos sobre la hipotenusa.

 

 

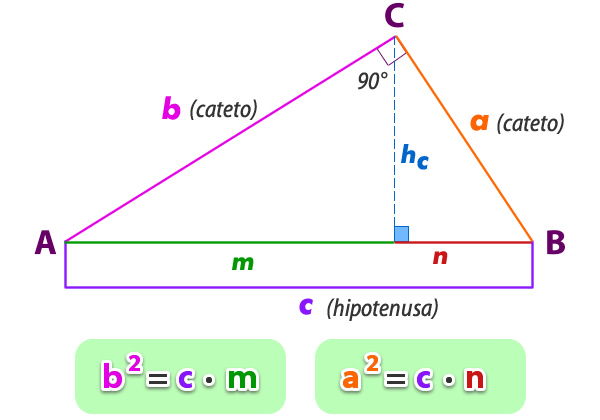
b) El cuadrado de la medida de uno de los catetos es igual al producto de su proyección sobre la hipotenusa y la medida de la hipotenusa completa.

 

 

1.12- Teorema particular de Thales o fundamental de la semejanza

A raíz del concepto de semejanza basado en las proporciones entre la pirámide y su bastón, surge el “teorema fundamental de la semejanza entre triángulos”, o también conocido como “teorema particular de Thales.”

Este teorema trata sobre los segmentos proporcionales que son determinados por dos paralelas.

 

a. Primer enunciado:

Al cortar los lados de un ángulo cualquiera por dos paralelas, los segmentos de los lados del ángulo determinados por las paralelas son proporcionales.

 

 

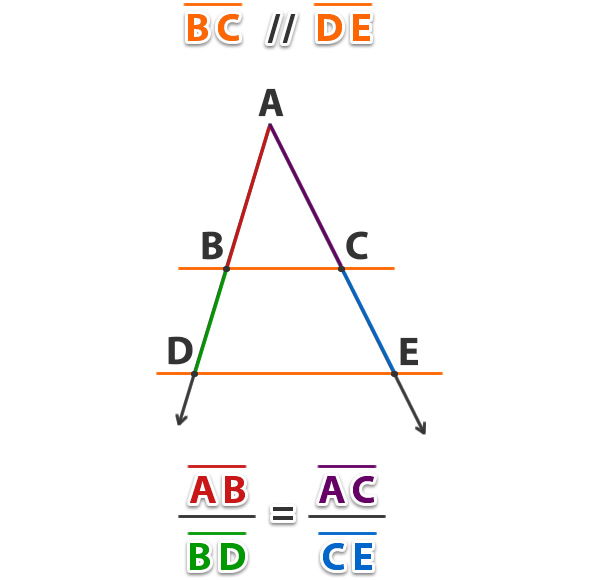
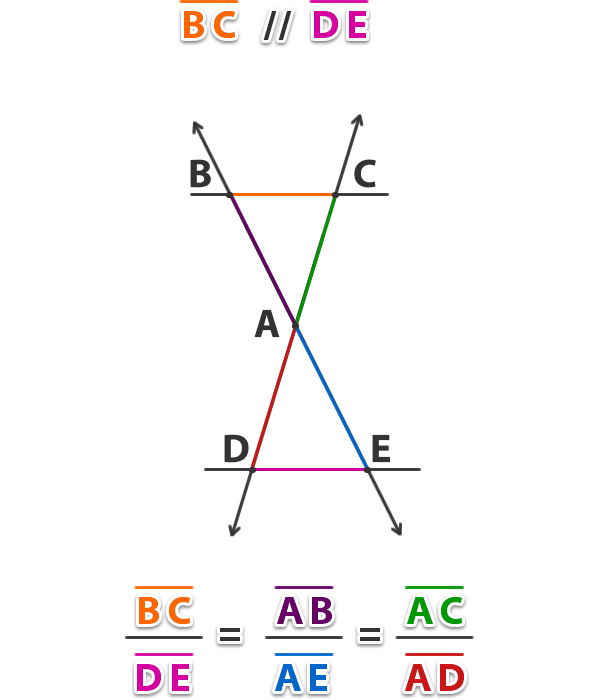
Ejemplo: Si las rectas BC y DE son paralelas, determina el valor de x para la siguiente figura;

 

 

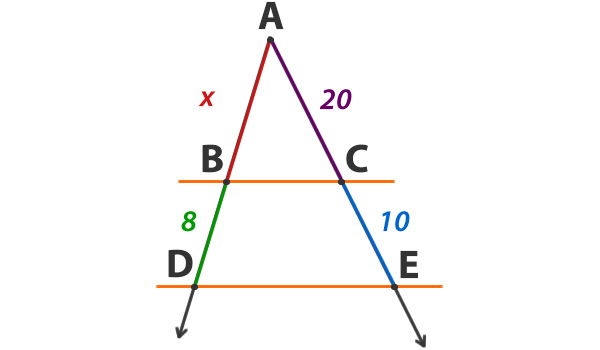
Aplicamos el teorema;

 

 

Respuesta: La recta AB (x) mide 16.

 

b. Segundo enunciado:

Al cortar los lados de un ángulo cualquiera por dos paralelas, los segmentos que se forman desde el vértice a los puntos de intersección de las paralelas son proporcionales entre sí. 

 

 

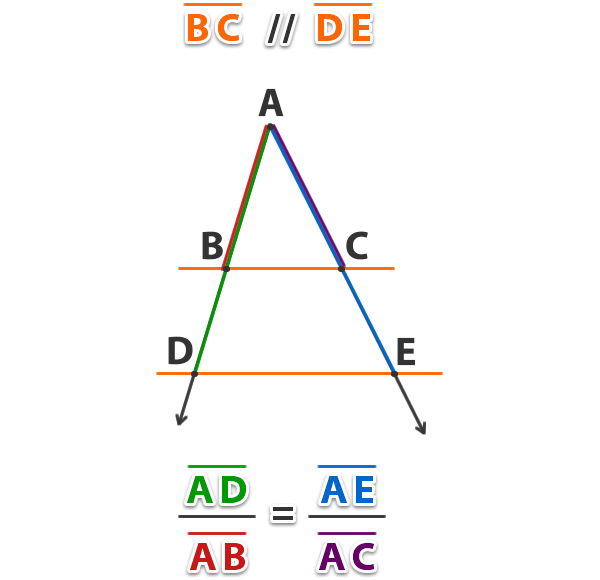
Ejemplo: 

Si BC // DE y AD = 16, AE = 24 y AB = 2, determina el valor de la recta AC en la siguiente figura;

 

 

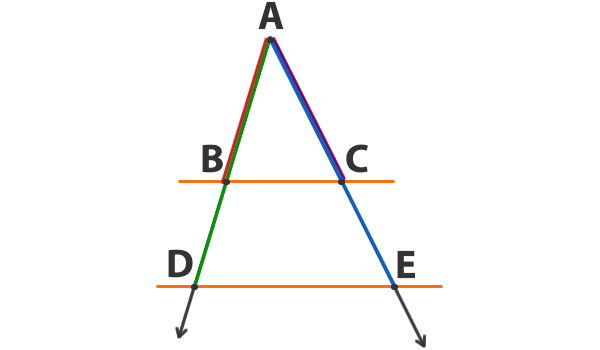
Aplicamos el teorema;

 

 

Respuesta: La recta AC mide 3.

 

c. Tercer enunciado:

Al cortar los lados de un ángulo cualquiera por dos paralelas, estas son entre sí como los segmentos medios desde el vértice a las paralelas. 

 

 

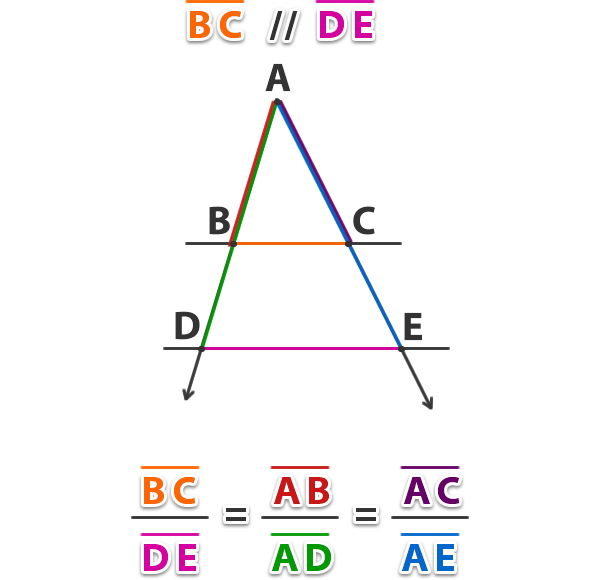
Ejemplo: Determina el valor de x para que L₁ y L₂ sean paralelas;

 

 

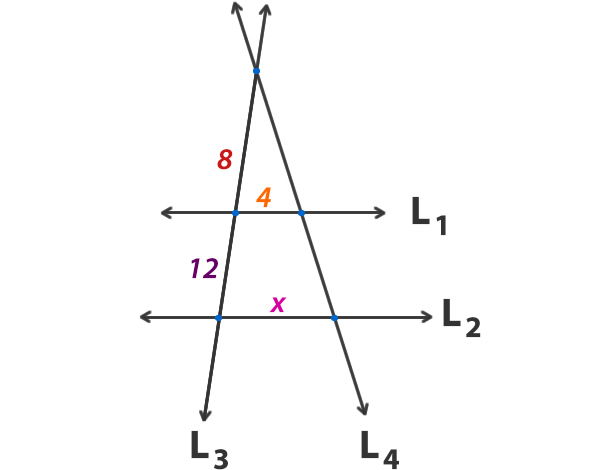
Hay ejercicios como este, que pueden parecer más difíciles, ya que el vértice y las intersecciones con las paralelas no tienen letras, pero si lees el enunciado del teorema, te darás cuenta de que es igual de sencillo, observa;

Para determinar el valor de x consideramos que L₁ y L₂ son paralelas que cortan los lados del triángulo, entonces, definiremos los segmentos en L₃ desde el vértice a las paralelas (que es donde están los datos).

 

 

Ahora escribimos la proporción, según el teorema; 

 

 

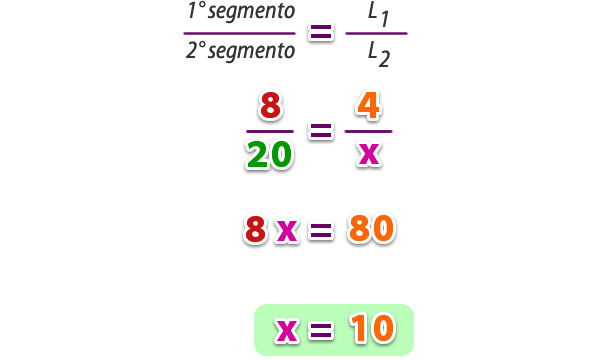
Respuesta: El valor de x es 10.

 

- Este mismo teorema se aplica a paralelas que cortan las extensiones de los lados más allá del vértice, donde podemos aplicar la siguiente proporción;

 

 

 

Ejemplo:

Si L₁ // L₂ // L₃ determina la medida de a.

 

 

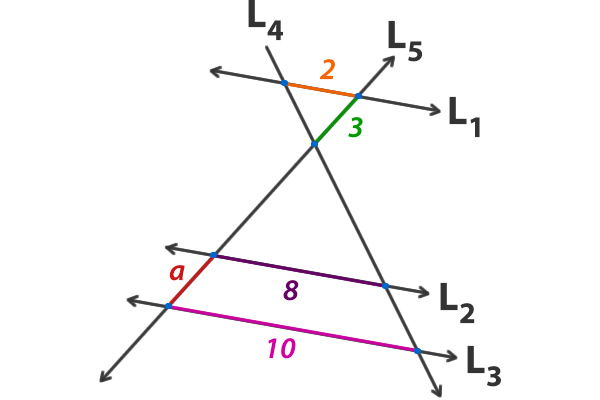
Para resolver este ejercicio, debemos aplicar el teorema de Thales en dos ocasiones y luego restar, para lo cual definiremos como x e y, los segmentos que vamos a calcular;

 

 

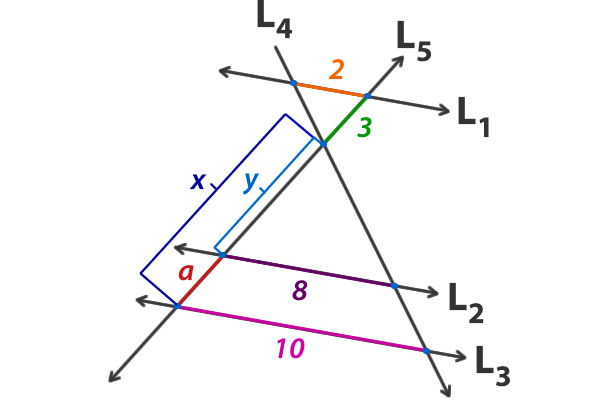
Escribimos las proporciones según el teorema y calculamos;

 

 

Ahora restamos para obtener la medida de a.

 

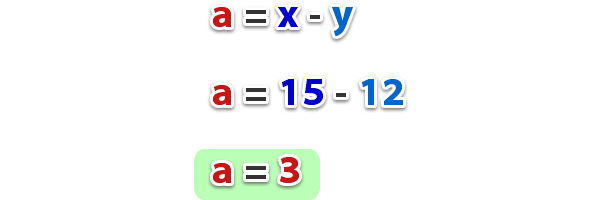
Respuesta: La medida de a es 3.

 

3- Teorema General de Thales

Al cortar dos o más rectas por tres o más paralelas, los segmentos determinados sobre las rectas son proporcionales entre sí.

 

 

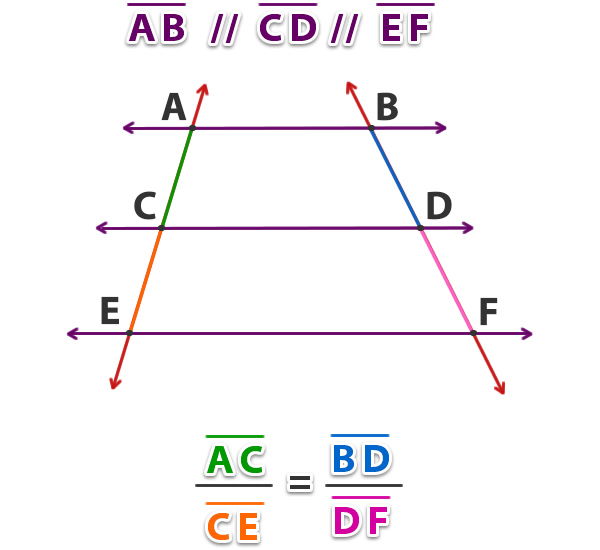
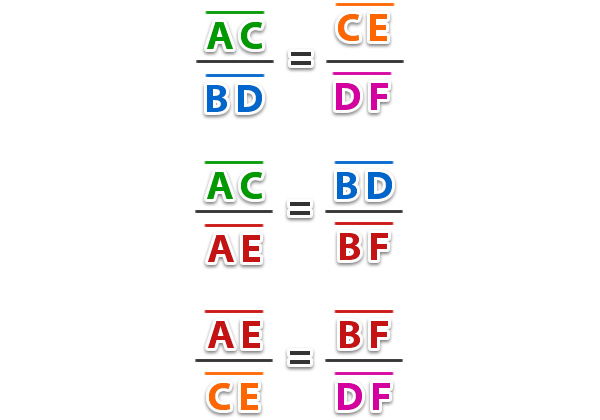
Del teorema general de Thales, se pueden obtener también las siguientes proporciones;

 

 

Ejemplo:

Si L₁ // L₂ // L₃, calcula a y b, si se sabe que a + b = 15

 

 

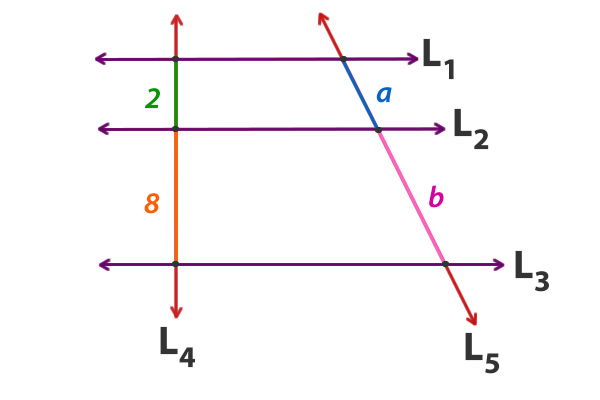
Establecemos la proporción para calcular b;

 

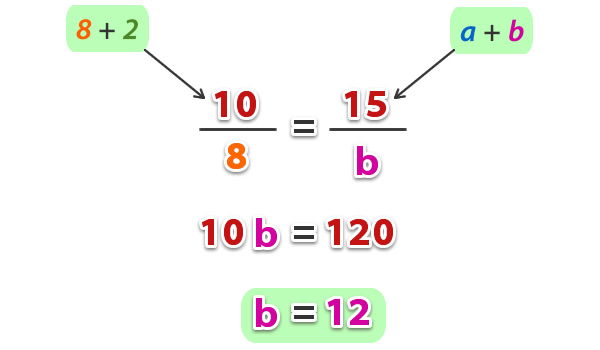
Ahora como a + b = 15, reemplazamos b y obtenemos el valor de a;

 

Respuesta: a = 3 y b = 12.

 

4 - Teorema recíproco de Thales.

Si dos o más rectas determinan segmentos proporcionales sobre dos transversales, entonces las rectas son paralelas entre sí. Es decir, es el inverso a los teoremas de Thales.

Ejemplos;

 

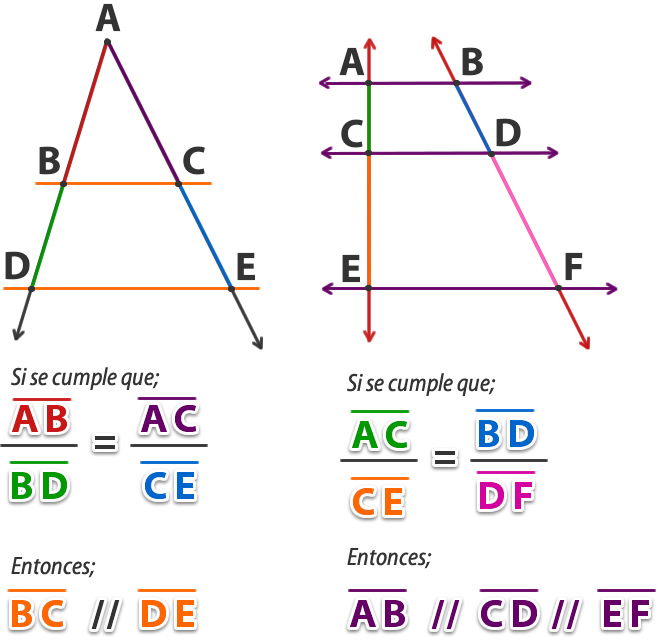
El teorema recíproco se cumple para todos los teoremas de Thales.

 

Dato: Recuerda que las aplicaciones del tema de Thales, nos sirven para resolver problemas de la vida cotidiana, especialmente para distancias inaccesibles, o que son muy difíciles de medir.

 

Ejemplo:

Nicolás mide 1,50 m. de altura, se encuentra a 1,20 m. de un poste que tiene encendida su luminaria a 3 m. del suelo, ¿cuál es el largo de la sombra que proyecta Nicolás?

 

 

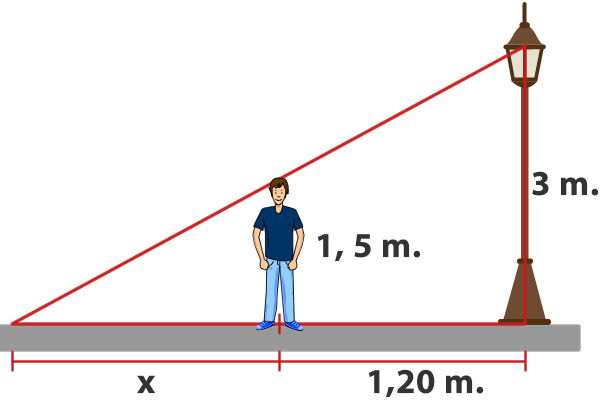
Aplicamos el teorema de Thales;

 

 

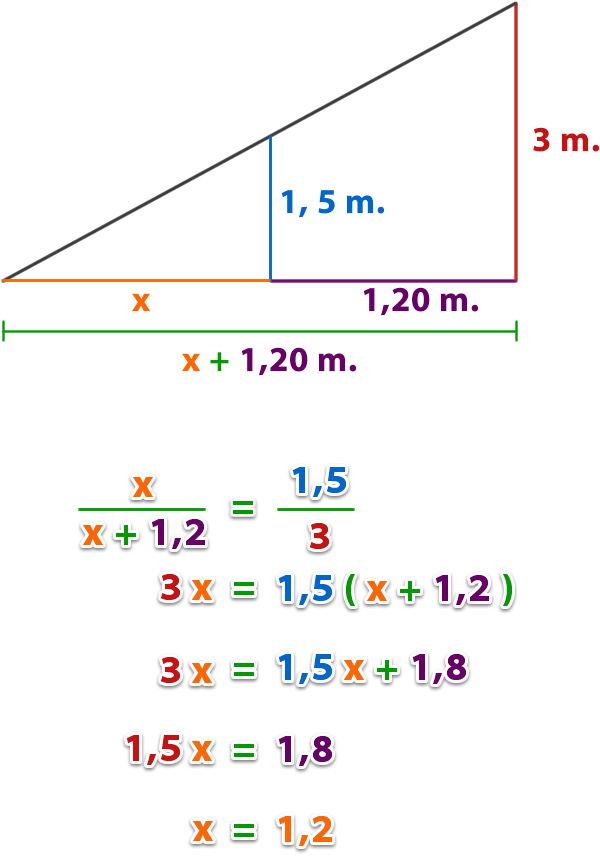
Respuesta: El largo de la sombra que proyecta Nicolás es de 1,20 m.