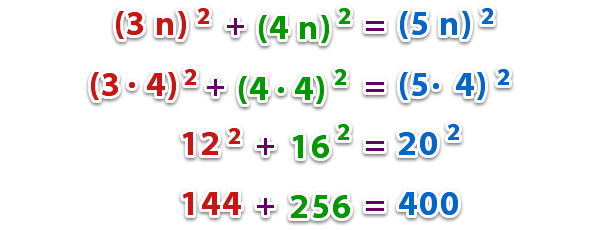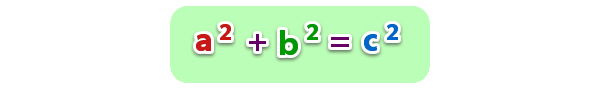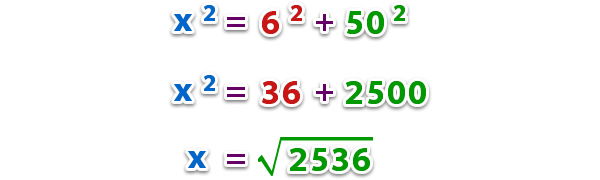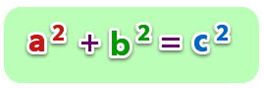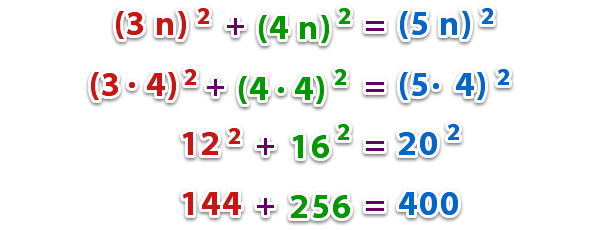1- Pitágoras

Pitágoras de Samos, fue un matemático y filósofo griego, nació en la isla de Samos, actual Grecia, en el año 572 a.C., fundó su escuela en Crotona en el sur de Italia. La escuela pitagórica era una sociedad o secta científica, religiosa y política. Los trabajos de los pitagóricos fueron desarrollados entre los años 585 a.C. y 400 a.C., existía un nivel de secreto en sus enseñanzas. Se dice que Pitágoras huyó a Metaponto, actual Italia, donde fue asesinado, en el año 497 a.C.

Pitágoras transformó las matemáticas en una enseñanza liberal, ya que sus resultados se formaban abstractamente, sin un contexto material, como es el famoso teorema de Pitágoras, que establece la relación entre los lados de un triángulo rectángulo, el cual se utilizaba incluso en civilizaciones anteriores a la griega. Este teorema se encuentra enunciado en el libro I, proposición 48, de los elementos de Euclides.

 

2- Teorema de Pitágoras

En todo triángulo rectángulo, el cuadrado de la hipotenusa (lado opuesto al ángulo recto) es igual a la suma de los cuadrados de los catetos (lados que componen el ángulo recto).

 

 

 

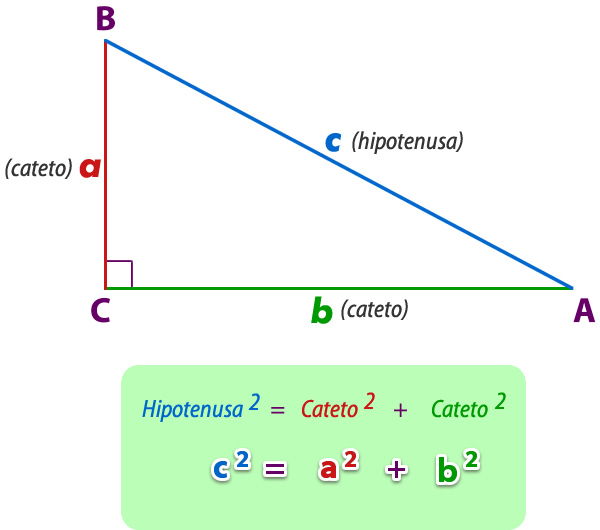
Para entender mejor este teorema mira la siguiente representación donde se relacionan las áreas;

 

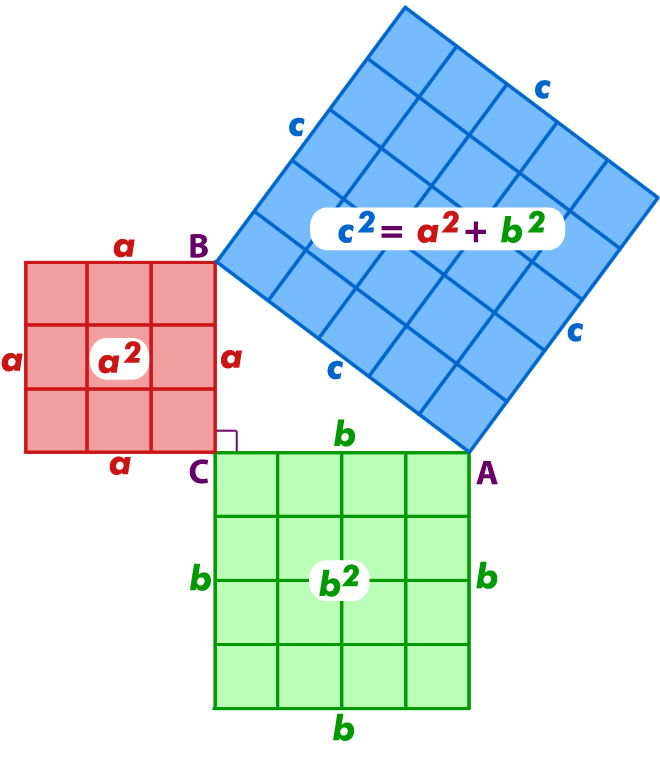
En todo triángulo rectángulo, el área del cuadrado construido sobre la hipotenusa es igual a la suma de las áreas de los cuadrados construidos sobre los catetos.

 

2.1- Recíproco del teorema de Pitágoras:

Del teorema principal de Pitágoras, se desprende el recíproco; Si en un triángulo, la suma de los cuadrados de dos de sus lados es igual al cuadrado del tercer lado (el lado mayor), entonces es un triángulo rectángulo.

Dado el Δ ABC;

 

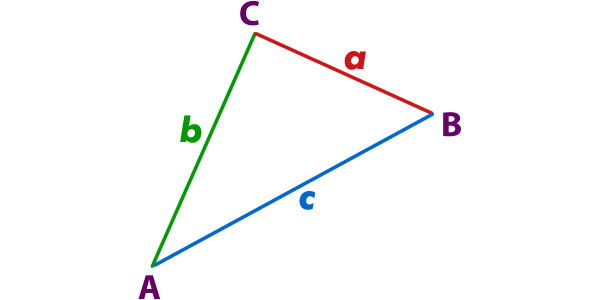
Si se cumple que; 

 

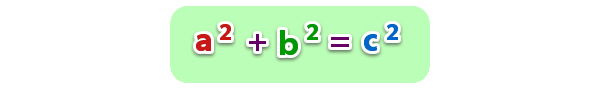
Entonces es un triángulo rectángulo es C.

 

Ejemplo:

Si un volantín ha quedado enredado en un poste de 6 metros de altura y el niño que lo tenía ha dejado el carrete en el suelo a 50 metros de este. ¿Cuánto hilo pierde si lo corta?

Primero puedes hacer un dibujo con lo que plantea el problema;

 

 

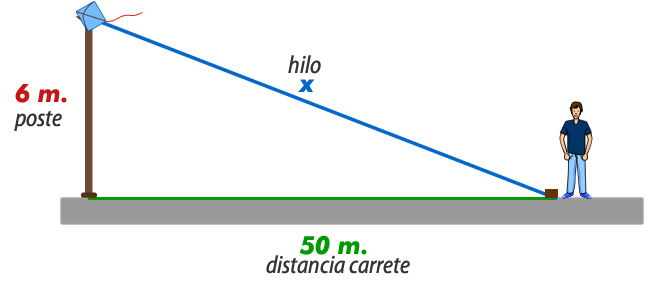
Para resolver este ejercicio podemos ocupar el teorema de Pitágoras de la siguiente forma;

 

 

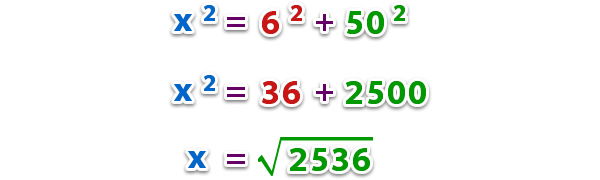
Respuesta: Si  lo corta pierde  la raíz de 2536 m.

2.2- Calcular la medida de uno de los lados del triángulo rectángulo conociendo la medida de los otros dos.

Si se conocen las medidas de dos lados de un triángulo se puede calcular la medida del tercer lado aplicando el Teorema de Pitágoras.

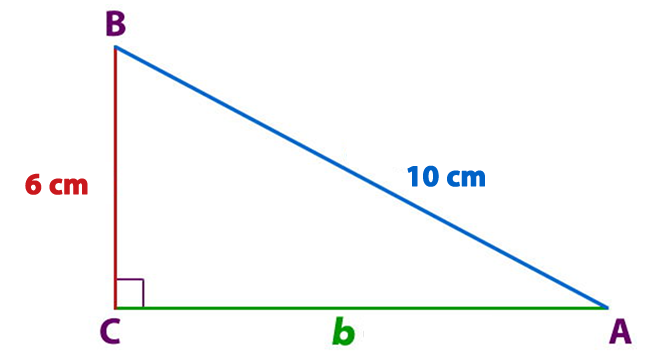
Caso 1: Si tenemos las medidas de a y c, ¿cómo se puede calcular la medida de b?

 

 

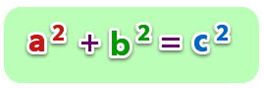
Despejamos el valor de b y la expresión queda de la siguiente manera.

 

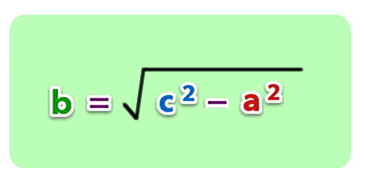
Luego, reemplazamos los valores en la expresión:
a= 6 cm
c= 10 cm

 

$$\begin{gathered} b =\hspace{0.17em}\sqrt{c^2- a^2} \\ b =\hspace{0.17em}\sqrt{{10}^2- 6^2} \\ b =\hspace{0.17em}\sqrt{100 - 36} \\ b =\hspace{0.17em}\sqrt{64} \\ b =\hspace{0.17em}8 \end{gathered}$$

¿Cómo se puede verificar si la medida del cateto es correcta?
Se puede verificar la medida mediante una construcción de un triángulo rectángulo. A continuación, se presentan los pasos a seguir:

Paso 1: Dibuja los segmentos de la hipotenusa y la medida del cateto conocido.

 

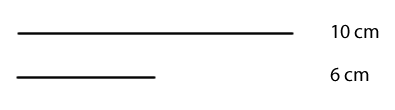
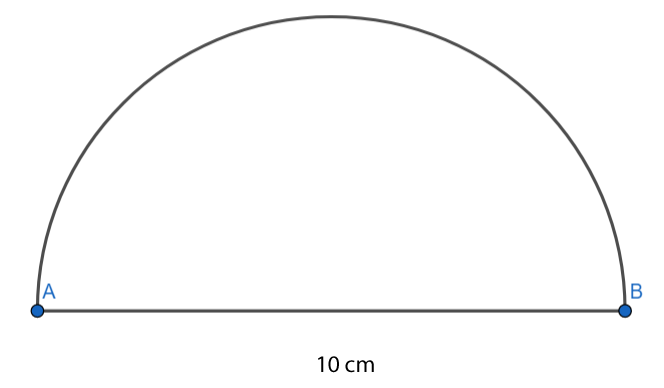
Paso 2: Traza la medida del segmento que representa a la hipotenusa. En este caso, debe ser de 10 cm.

 

Paso 3: Con el compás dibuja una semicircunferencia, cuyo diámetro será la medida de la hipotenusa.

 

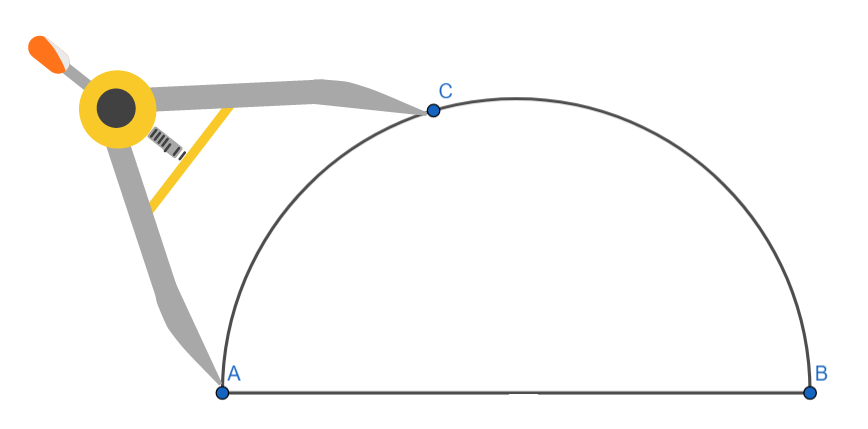
Paso 4: Con el compás ubicado en uno de los extremos del segmento de 10 cm traza una línea con la medida del cateto conocido, es decir, 6 cm. La línea debe coincidir con la semicircunferencia.

 

 

Paso 5: Une todos los vértices y verifica si la medida del otro cateto es de 8 cm.

 

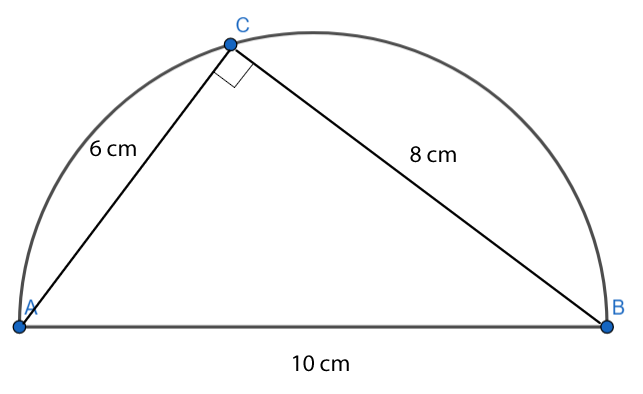
Al construir el triángulo rectángulo se puede verificar que las medidas de sus lados son correctas.

Caso 2:

Si tenemos las medidas de b y c, ¿cómo se puede calcular la medida de a?

 

 

 

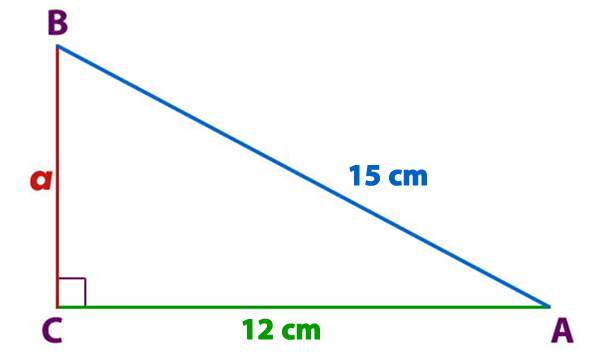
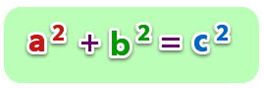
Despejamos a y la expresión queda de la siguiente manera:

 

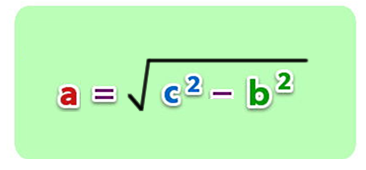
Reemplazamos los valores de b y c en la expresión:
b= 12 cm
c= 15 cm

 

$$\begin{gathered} a =\hspace{0.17em}\sqrt{c^2 - b^2} \\ a =\hspace{0.17em}\sqrt{{15}^2 - {12}^2} \\ a =\hspace{0.17em}\sqrt{225 - 144} \\ a =\hspace{0.17em}\sqrt{81} \\ a =\hspace{0.17em}9 \end{gathered}$$

 

La medida del cateto a es de 9 cm.
 

Si tenemos las medidas de un triángulo, ¿cómo podemos conocer si corresponden a las medidas de un triángulo rectángulo?

Para saber la respuesta podemos aplicar el teorema de Pitágoras.

a) Triángulo de lados 4 cm, 8 cm y 10 cm.

$$\begin{gathered} 4^2 + 8^2 \square {10}^2 \\ 16 + 64 \square 100 \\ 80 \ne 100 \end{gathered}$$
 

No se cumple el teorema de Pitágoras, por lo tanto, no es rectángulo.
 

b) Triángulo de lados 5 cm, 12 cm y 13 cm.

$$\begin{gathered} 5^{2 }+{12}^2 \square {13}^2 \\ 25 + 144 \square 169 \\ 169 = 169 \end{gathered}$$

Se cumple el teorema de Pitágoras, por lo tanto, es un triángulo rectángulo.
 

c) Triángulo de lados 8 cm, 15 cm y 17 cm.

$$\begin{gathered} 8^2 +{15}^2 \square {17}^2 \\ 64 + 225 \square 289 \\ 289 = 289 \end{gathered}$$

 

Se cumple el teorema de Pitágoras, por lo tanto, es un triángulo rectángulo.

 

2.3- Ejercicios resueltos

a) ¿Cuál es el perímetro del siguiente triángulo rectángulo?

 

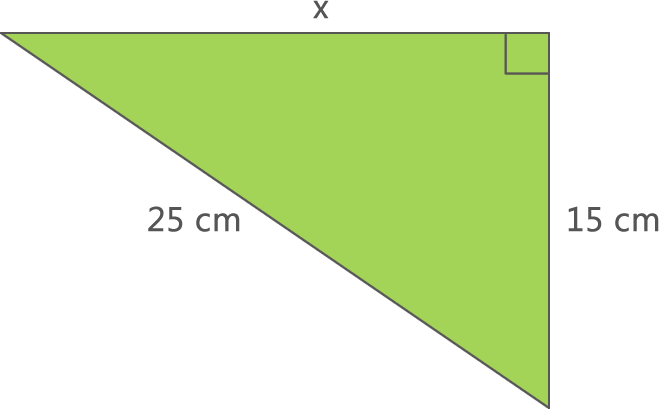
En este caso tenemos que determinar la medida del lado faltante del triángulo rectángulo, para ello aplicamos la siguiente fórmula:

 

$$\begin{gathered} x =\sqrt{{25}^2 - {15}^2} \\ x =\sqrt{625 - 225} \\ x =\sqrt{400} \\ x = 20 cm \end{gathered}$$

El otro cateto mide 20 cm.

A continuación, calculamos el perímetro sumando las medidas de todos los lados del triángulo:
 

$$\begin{gathered} P = 15 + 20 + 25 \\ P = 60 cm \end{gathered}$$

 

b) Calcular la medida de la diagonal de un cuadrado cuyo lado mide 6 cm.

 

 

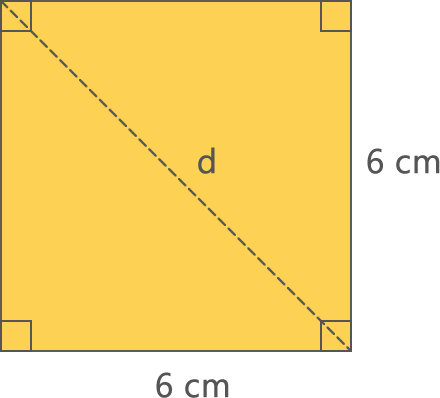
Al trazar una diagonal del cuadrado se forman dos triángulos rectángulos isósceles. Los catetos corresponden a las medidas de los lados del cuadrado y la hipotenusa, a la diagonal.

Aplicando el teorema de Pitágoras tenemos lo siguiente:

$$\begin{gathered} d^2 = 6^2 + 6^2 \\ {d}^2 = 36 + 36 \\ {d}^2 = 72 \\ d = \sqrt{72} \\ d \approx 8,49 \end{gathered}$$

 

La diagonal del cuadrado de lado 6 cm mide 8,49 cm aproximadamente.

 

3- Números pitagóricos

Son aquellos tríos de números enteros positivos (a, b y c) que cumplen con el teorema de Pitágoras.  Es decir, estos números cumplen que, a² + b² = c².

La terna pitagórica más pequeña es 3, 4 y 5. Es fácil ver que 3² + 4² = 25² (9 + 16 = 25).

Otras ternas pitagóricas; (5,12,13), (8,15,17), (9,40,41)…Las ternas pitagóricas son infinitas, las que se pueden demostrar con la primera terna pitagórica;

Sea n un número entero mayor que 1, diremos que 3 n, 4 n y 5 n son una terna pitagórica ya que;

 

Así por ejemplo si n = 4 tenemos que; la terna pitagórica seria (12, 16, 20), si verificamos: